题目内容
13.函数y=$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sinxcosx+1,x∈R(1)当函数y取得最大值时,求自变量的取值集合;
(2)该函数的图象可由y=sinx的图象经过怎样的平移和伸缩变换得到?
(3)试用“五点”法作出函数在长度为一个周期的闭区间上的简图.
分析 (1)利用二倍角的正弦、余弦函数公式化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数最大值为1,求出y的最大值,以及此时x的取值集合;
(2)先ω,再φ,后A,利用函数y=Asin(ωx+φ)的图象变换规律即可得解.
(3)列表,令 2x+$\frac{π}{6}$分别等于0,$\frac{π}{2}$,π,$\frac{3π}{2}$,2π,求得对应的x,y值,以这五对x,y值作为点的坐标,在坐标系中描出,用平滑曲线连接,即得它在一个周期内的闭区间上的图象.
解答 解:(1)∵y=$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sinxcosx+1
=$\frac{1+cos2x}{4}$+$\frac{\sqrt{3}}{4}$sin2x+1
=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)+$\frac{5}{4}$,
∴当2x+$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈Z,即x=kπ+$\frac{π}{6}$,k∈Z时,sin(2x+$\frac{π}{6}$)取得最大值1,y取得最大值$\frac{7}{4}$;
(2)将函数y=sinx的图象上每一个点的横坐标变为原来的$\frac{1}{2}$倍(纵坐标不变),再将图象向左平移$\frac{π}{12}$个单位长度,再将图象上每一个点的纵坐标变为原来的$\frac{1}{2}$倍(横坐标不变);最后在整体向上平移$\frac{5}{4}$个单位即可得到函数f(x)的图象.
(3)列表:
| 2x+$\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $-\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| y=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)+$\frac{5}{4}$ | 0 | 3 | 0 | -3 | 0 |
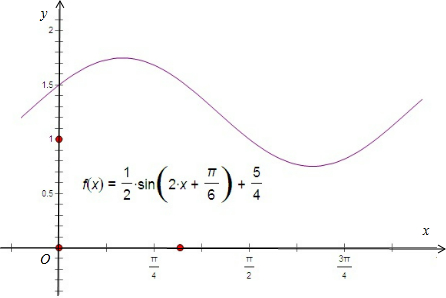
点评 本题主要考查了三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换,正弦函数的图象和性质,属于基本知识的考查.

 名校课堂系列答案
名校课堂系列答案| A. | 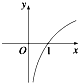 | B. | 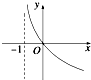 | C. | 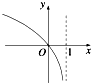 | D. |  |
| A. | $\frac{1}{21}$ | B. | $\frac{1}{23}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{27}$ |
| A. | $\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}\right.$ | B. | $\left\{\begin{array}{l}x'=3x\\ y'=2y\end{array}\right.$ | C. | $\left\{\begin{array}{l}x'=\frac{1}{2}x\\ y'=\frac{1}{3}y\end{array}\right.$ | D. | $\left\{\begin{array}{l}x'=\frac{1}{3}x\\ y'=\frac{1}{2}y\end{array}\right.$ |