题目内容
2.已知在数列{an}中,a1=1,an=$\frac{{a}_{n-1}}{2{a}_{n-1}+1}$,则a12等于( )| A. | $\frac{1}{21}$ | B. | $\frac{1}{23}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{27}$ |
分析 由递推公式依次求出数列的前四项由此猜想${a}_{n}=\frac{1}{2n-1}$.再用数学归纳法进行证明,从而能求出a12.
解答 解:∵在数列{an}中,a1=1,an=$\frac{{a}_{n-1}}{2{a}_{n-1}+1}$,
∴${a}_{2}=\frac{1}{2+1}$=$\frac{1}{3}$,
${a}_{3}=\frac{\frac{1}{3}}{2×\frac{1}{3}+1}$=$\frac{1}{5}$,
${a}_{4}=\frac{\frac{1}{5}}{2×\frac{1}{5}+1}$=$\frac{1}{7}$,
由此猜想${a}_{n}=\frac{1}{2n-1}$.
①当n=1时,${a}_{1}=\frac{1}{2×1-1}$=1,成立.
②假设n=k(k≥2)时,${a}_{k}=\frac{1}{2k-1}$成立,
则当n=k+1时,${a}_{k+1}=\frac{{a}_{k}}{2{a}_{k}+1}$=$\frac{\frac{1}{2k-1}}{\frac{2}{2k-1}+1}$=$\frac{1}{2+2k-1}$=$\frac{1}{2(k+1)-1}$,也成立,
∴${a}_{n}=\frac{1}{2n-1}$,
∴a12=$\frac{1}{2×12-1}$=$\frac{1}{23}$.
故选:B.
点评 本题考查数列的第12项的求法,是中档题,解题时要认真审题,注意递推思想和数学归纳法的合理运用.

练习册系列答案
相关题目
10.数列{an}中,a1=1,a1•a2…an=n2,则a3-a5=( )
| A. | $\frac{1}{16}$ | B. | -$\frac{1}{16}$ | C. | $\frac{11}{16}$ | D. | -$\frac{11}{16}$ |
17.某程序框图如图所示,该程序运行后输出的S的值是( )
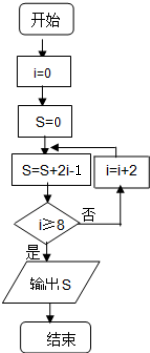

| A. | 20 | B. | 35 | C. | 40 | D. | 45 |
11.曲线y=x2-2x与直线x=-1,x=1以及x轴所围图形的面积为( )
| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |