题目内容

8．已知长方体ABCD-A1B1C1D1内接于球O，底面ABCD是边长为2的正方形，平面AOB与平面ABCD所成角为60°，则球O的表面积为20π．

分析 利用底面ABCD是边长为2的正方形，平面AOB与平面ABCD所成角为60°，可得长方体的高为2$\sqrt{3}$，即可求出长方体的对角线的长，可得球O的半径，即可求出球O的表面积．

解答 解：∵底面ABCD是边长为2的正方形，平面AOB与平面ABCD所成角为60°，
∴长方体的高为2$\sqrt{3}$，
∴长方体的对角线的长为$\sqrt{{2}^{2}+{2}^{2}+（2\sqrt{3}）^{2}}$=2$\sqrt{5}$，
∴球O的半径为$\sqrt{5}$，
∴球O的表面积为4π•5=20π．
故答案为：20π．

点评 本题考查球O的表面积，考查面面角，正确求出球O的半径是关键．

练习册系列答案
相关题目
8．已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的坐标，求$\overrightarrow{a}•\overrightarrow{b}$．
（1）$\overrightarrow{a}$=（4，-5），$\overrightarrow{b}$=（-4，3）；
（2）$\overrightarrow{a}$=（3，5），$\overrightarrow{b}$=（-5，3）；
（3）$\overrightarrow{a}$=（8，5），$\overrightarrow{b}$=（-7，-8）；
（4）$\overrightarrow{a}$=（12，-7），$\overrightarrow{b}$=（4，-1）．
9．设函数f（x）=log（n+1）（n+2），n∈N*．
（1）求f（1）•f（2）和f（1）•f（2）•f（3）•f（4）•f（5）•f（6）的值；
（2）若把使f（1）•f（2）…f（k）为整数的正整数k叫做企盼数．试求f（1）•f（2）…f（k）=2014的企盼数k．
16．已知三个函数f（x）=2x+x，g（x）=x-2，h（x）=log2x+x的零点依次为a，b，c，则（　　）
A．a＜b＜cB．a＜c＜bC．b＜a＜cD．c＜a＜b
3．设f（x）=sinxcosx-cos2（x+$\frac{π}{4}$），求f（x）的最小正周期．
13．函数y=$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sinxcosx+1，x∈R
（1）当函数y取得最大值时，求自变量的取值集合；
（2）该函数的图象可由y=sinx的图象经过怎样的平移和伸缩变换得到？
（3）试用“五点”法作出函数在长度为一个周期的闭区间上的简图．
20．如图，直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直，AB∥CD，AB⊥BC，AB=2CD=2BC=2，EA⊥EB．
（1）求直线EC与平面ABE所成角的正弦值；
（2）线段EA上是否存在点F，使CE∥平面FBD？若存在，求出$\frac{EF}{EA}$；若不存在，请说明理由．
17．某程序框图如图所示，该程序运行后输出的S的值是（　　）
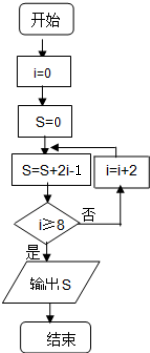
A．20B．35C．40D．45
18．二次函数f（x）=ax2+bx+c（x∈R）的部分对应值如表：
x-3-2-101234
y6m-4-6-6-4n6
可以判断方程ax2+bx+c=0的两根所在的区间是（　　）
A．（-3，-1）和（2，4）B．（-3，-1）和（-1，1）C．（-1，1）和（1，2）D．（-1，3）和（4，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网