题目内容
3.将圆x2+y2=1变换为椭圆$\frac{{{{x'}^2}}}{4}+\frac{{{{y'}^2}}}{9}=1$的伸缩变换公式为( )| A. | $\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}\right.$ | B. | $\left\{\begin{array}{l}x'=3x\\ y'=2y\end{array}\right.$ | C. | $\left\{\begin{array}{l}x'=\frac{1}{2}x\\ y'=\frac{1}{3}y\end{array}\right.$ | D. | $\left\{\begin{array}{l}x'=\frac{1}{3}x\\ y'=\frac{1}{2}y\end{array}\right.$ |
分析 通过x与x′,y与y′的数值关系,即可把圆x2+y2=1变成椭圆$\frac{{{{x'}^2}}}{4}+\frac{{{{y'}^2}}}{9}=1$,得到伸缩变换.
解答 解:对于圆x2+y2=1的方程,令$\left\{\begin{array}{l}x=\frac{x′}{2}\\ y=\frac{y′}{3}\end{array}\right.$,
即为把圆x2+y2=1变成椭圆$\frac{{{{x'}^2}}}{4}+\frac{{{{y'}^2}}}{9}=1$,伸缩变换为:$\left\{\begin{array}{l}x′=2x\\ y′=3y\end{array}\right.$.
故选:A.
点评 本题考查了圆变换为椭圆的伸缩变换,考查了变形能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.曲线y=x2-2x与直线x=-1,x=1以及x轴所围图形的面积为( )
| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
18.二次函数f(x)=ax2+bx+c(x∈R)的部分对应值如表:
可以判断方程ax2+bx+c=0的两根所在的区间是( )
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | m | -4 | -6 | -6 | -4 | n | 6 |
| A. | (-3,-1)和(2,4) | B. | (-3,-1)和(-1,1) | C. | (-1,1)和(1,2) | D. | (-1,3)和(4,+∞) |
8.如图所示,在“推理与证明”的知识结构图中,如果要加入“综合法”,则应该放在( )
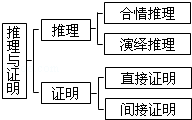

| A. | “合情推理”的下位 | B. | “直接证明”的下位 | ||
| C. | “演绎推理”的下位 | D. | “间接证明”的下位 |
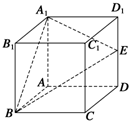 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.