题目内容

已知在△ABC中，∠B=
π
3
，AC边上的中线BD长为2，求该三角形面积最大值．
考点：正弦定理
专题：综合题,解三角形,不等式的解法及应用
分析：设AB=x，AC=y，利用余弦定理，结合平行四边形对角线的平方和等于四条边的平方和，可得x2+y2+xy=16，由基本不等式可得xy的最大值，再利用三角形的面积公式，即可得出结论．
解答： 解：设AB=x，AC=y，则根据余弦定理可得AC2=x2+y2-2xycos
π
3
=x2+y2-xy，①
根据平行四边形对角线的平方和等于四条边的平方和，可得AC2+42=2（x2+y2），②
由①②可得x2+y2+xy=16
由基本不等式可得x2+y2+xy=16≥3xy，
∴xy≤
16
3
，
∴xy的最大值为
16
3
，
∴三角形面积最大值为
1
2
•
16
3
•sin
π
3
=
4
3
3
．
点评：本题考查余弦定理，考查平行四边形对角线的平方和等于四条边的平方和，考查基本不等式，考查三角形的面积公式，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
函数fM（x）的定义域为R，且定义如下：fM(x)=
1，x∈M
-1，x∉M
（其中M是非空实数集）．若非空实数集A，B满足A∩B=∅，则函数g（x）=fA∪B（x）+fA（x）•fB（x）的值域为
 
．
已知函数f（x）=asinx•cosx+
3
cos2x，x∈R，f（
π
3
）=0．
（1）求常数a的值；
（2）求f（x）的最大值．
设a∈R，函数f（x）=x2e1-x-a（x-1）．
（Ⅰ）当a=1时，求f（x）在（
3
4
，2）内的极大值；
（Ⅱ）设函数g（x）=f（x）+a（x-1-e1-x），当g（x）有两个极值点x1，x2（x1＜x2）时，总有x2g（x1）≤λf′（x1），求实数λ的值．（其中f′（x）是f（x）的导函数．）
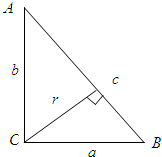设直角△ABC的直角边BC=a，AC=b，斜边AB=c，且a＜b，现分别以直线BC，AC和AB为轴将直角△绕轴旋转一周，所得三个旋转体体积分别为V1，V2和V3，试比较V1，V2，V3的大小．
已知cos（15°+α）=
3
5
，α为锐角，求：
tαn(435°-α)+sin(α-165°)
cos(195°+α)×sin(105°+α)
．
已知tanα=2，求sin2α+2cos2α-sinαcosα+1的值．
求函数y=lg（x3-27x）的单调区间．
在RT△ABC中，∠C=90°，AC=b，BC=a（a＜b﹚，分别绕BC，AC，AB旋转三角形得三个旋转体，其体积Va，Vb，Vc的大小顺序是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网