题目内容
求函数f(x)=x2+
(x≤-
)的值域.
| 1 |
| x |
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值,函数的值域
专题:导数的综合应用
分析:解:本题考查利用导函数来判断函数的单调性,再求函数的值域.也可以利用函数的单调性定义来判断函数的单调性.
解答:
解:f′(x)=2x-
=
在x≤-
时f′(x)<0,所以函数单调递减,f(x)≥f(-
)=-
,
所以函数的值域为:[-
,+∞).
故答案为:[-
,+∞).
| 1 |
| x2 |
| 2x3-1 |
| x2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
所以函数的值域为:[-
| 7 |
| 4 |
故答案为:[-
| 7 |
| 4 |
点评:导数作为一个工具,是高中阶段的一个重点内容,根据导数的正负性来决定函数的单调性,是常考题型.

练习册系列答案
相关题目
设平面上有四个相异的点A、B、C、D,已知(
+
-2
)•(
-
)=0,则△ABC的形状是( )
| DB |
| DC |
| DA |
| DB |
| DC |
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
已知集合A={x||x+1|<1},B={x|y=
,y∈R},则A∩∁RB=( )
(
|
| A、(-2,1) |
| B、(-2,-1] |
| C、(-1,0) |
| D、[-1,0) |
运行如图所示的程序框图,则输出S的值为( )


| A、8 | B、4 | C、3 | D、-2 |
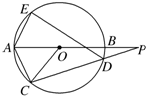 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC.
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC.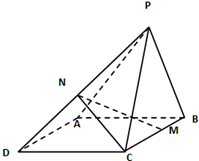 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,AB=2,△PCB为正三角形,且平面PCB⊥平面ABCD,M,N分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,AB=2,△PCB为正三角形,且平面PCB⊥平面ABCD,M,N分别为BC,PD的中点.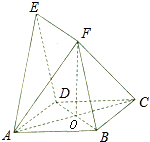 如图,四边形ABCD与BDEf均为菱形,已知∠DAB=∠DBF=60°,且面ABCD⊥面BDEF,AC=2
如图,四边形ABCD与BDEf均为菱形,已知∠DAB=∠DBF=60°,且面ABCD⊥面BDEF,AC=2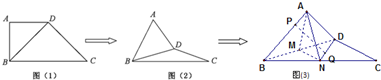 在直角梯形ABCD中,AD∥BC,
在直角梯形ABCD中,AD∥BC,