题目内容
18.已知函数$f(x)=\sqrt{{x^2}-2}+3\sqrt{2-{x^2}}$,则( )| A. | 奇函数而非偶函数 | B. | 偶函数而非奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
分析 求出函数的定义域,然后判断函数的奇偶性.
解答 解:函数$f(x)=\sqrt{{x^2}-2}+3\sqrt{2-{x^2}}$的定义域为:{$-\sqrt{2},\sqrt{2}$}.
函数的值域:{0}.
所以函数既是奇函数又是偶函数.
故选:C.
点评 本题考查函数的奇偶性的判断,基本知识的考查.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
10.已知函数f(x)=-x2+2ax+1-a在区间[0,1]上的最大值为2,则a的值为( )
| A. | 2 | B. | -1或-3 | C. | 2或-3 | D. | -1或2 |
6.若a为实数,且2+ai=(1+i)(3+i),则a=( )
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
13.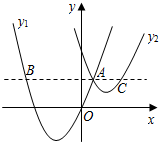 如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2-y1=4;
④2AB=3AC.
其中正确结论是( )
 如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2-y1=4;
④2AB=3AC.
其中正确结论是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
3.满足{-1,0}∪A={-1,0,1}的集合A共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列命题正确的是( )
| A. | 很大的实数可以构成集合 | |
| B. | 自然数集N中最小的数是1 | |
| C. | 集合{y|y=x2-1}与集合{(x,y)|y=x2-1}是同一个集合 | |
| D. | 空集是任何集合的子集. |
7.若非零实数x,y,z满足2x=3y=6z,则$\frac{x+y}{z}$∈( )
| A. | (5,6) | B. | (4,5) | C. | (3,4) | D. | (2,3) |
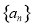 的前
的前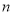 项和为
项和为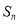 ,
,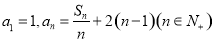 .
.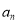 和
和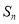 ;
; 的前
的前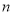 项和为
项和为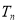 ,证明:
,证明: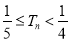 .
.