题目内容
18.二次函数f(x)=ax2+bx+c(x∈R)的部分对应值如表:| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | m | -4 | -6 | -6 | -4 | n | 6 |
| A. | (-3,-1)和(2,4) | B. | (-3,-1)和(-1,1) | C. | (-1,1)和(1,2) | D. | (-1,3)和(4,+∞) |
分析 确定f(-3)f(-1)<0,f(2)f(4)<0,利用零点存在性定理可以判断方程ax2+bx+c=0的两根所在的区间.
解答 解:由题意,f(-3)=6,f(-1)=-4,f(2)=-4,f(4)=6,
∴f(-3)f(-1)<0,f(2)f(4)<0,
∴可以判断方程ax2+bx+c=0的两根所在的区间是(-3,-1)和(2,4).
故选:A.
点评 本题考查零点存在性定理,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
9.若过点P(1,0),Q(2,0),R(4,0),S(8,0)作四条直线构成一个正方形,则该正方形的面积不可能等于( )
| A. | $\frac{16}{17}$ | B. | $\frac{36}{5}$ | C. | $\frac{26}{5}$ | D. | $\frac{196}{53}$ |
6.双曲线x2-4my2=4的实轴长是虚轴长的2倍,则实数m=( )
| A. | 1 | B. | $\frac{1}{16}$ | C. | $\frac{1}{2}$ | D. | 1或$\frac{1}{16}$ |
3.将圆x2+y2=1变换为椭圆$\frac{{{{x'}^2}}}{4}+\frac{{{{y'}^2}}}{9}=1$的伸缩变换公式为( )
| A. | $\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}\right.$ | B. | $\left\{\begin{array}{l}x'=3x\\ y'=2y\end{array}\right.$ | C. | $\left\{\begin{array}{l}x'=\frac{1}{2}x\\ y'=\frac{1}{3}y\end{array}\right.$ | D. | $\left\{\begin{array}{l}x'=\frac{1}{3}x\\ y'=\frac{1}{2}y\end{array}\right.$ |
10.有5本不同的语文书,4本不同的数学书,从中任意取出2本,那么下列各组中的两个事件是“互斥而不对立”是( )
| A. | “至少有一本是数学书”与“都是数学书” | |
| B. | “至少有一本是数学书”与“都是语文书” | |
| C. | “至少有一本是数学书”与“至少有1本是语文书” | |
| D. | “恰有1本是数学书”与“恰有2本是语文书” |
7.某几何体的三视图如图所示,则该几何体的体积为( )
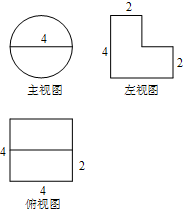

| A. | 4π | B. | 8π | C. | 12π | D. | 16π |