题目内容
15.在-20到40之间插入8个数,使这10个数成等差数列,则这10个数的和为( )| A. | 200 | B. | 100 | C. | 90 | D. | 70 |
分析 根据等差数列的前n项和公式计算即可.
解答 解:因为在-20到40之间插入8个数,使这10个数成等差数列,
所以根据等差数列前n项和公式,这10个数的和为:
S10=$\frac{10×(-20+40)}{2}$=100,
故选:B.
点评 本题考查了等差数列的前n项和公式,熟练掌握公式是解题的关键,本题是一道基础题.

练习册系列答案
相关题目
4.已知函数f(x)=$\left\{\begin{array}{l}{(a-2)x,x≥2}\\{(\frac{1}{2})^{x}-1,x<2}\end{array}\right.$,满足对任意的实数x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,则实数a的取值范围为( )
| A. | (-∞,2) | B. | [$\frac{13}{4}$,2) | C. | [$\frac{13}{8}$,2) | D. | (-∞,$\frac{13}{8}$] |
7.口袋中放有大小相等的2个红球和1个白球,有放回地每次摸取1个球,定义数列{an}:若第n次摸到红球,an=-1;若第n次摸到白球,an=1.如果Sn为数列{an}的前n项和,那么S7=3的概率为( )
| A. | $C_7^5×{({\frac{1}{3}})^2}×{({\frac{2}{3}})^5}$ | B. | $C_7^5×{({\frac{1}{3}})^2}×{({\frac{1}{3}})^5}$ | C. | $C_7^3×{({\frac{1}{3}})^2}×{({\frac{2}{3}})^5}$ | D. | $C_7^2×{({\frac{2}{3}})^2}×{({\frac{1}{3}})^5}$ |
5. 一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )
一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )
 一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )
一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )| A. | π+1 | B. | π+2 | C. | 2π+1 | D. | $3π+5+2\sqrt{2}$ |
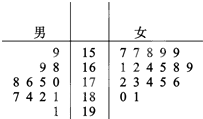 某部队为了在大阅兵中树立军队的良好形象,决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员,这30名军人的身高如图:单位:cm
某部队为了在大阅兵中树立军队的良好形象,决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员,这30名军人的身高如图:单位:cm