题目内容
已知函数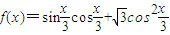
．，（Ⅰ）将f（x）写成Asin（ωx+φ）的形式，并求其图象对称中心的横坐标；
（Ⅱ）如果△ABC的三边a、b、c满足b2=ac，且边b所对的角为x，试求x的范围及此时函数f（x）的值域．
【答案】分析：（1）先将函数f（x）化简为：
，
令
=0，可得答案．
（2）由b2=ac，有根据余弦定理可得
，所以可得
，f（x）值域为
．得到答案．
解答：解：
，
（Ⅰ）由
=0
即
，k∈z，
即对称中心的横坐标为
π，k∈z；
（Ⅱ）由已知b2=ac，
，
∴
∵
，∴
，∴
，
即f（x）的值域为
，
综上所述，
，f（x）值域为
．
点评：本题主要考查三角函数的化简和余弦定理的应用．属中档题．求三角函数值域时一定多注意自变量x的取值范围．
，令
=0，可得答案．（2）由b2=ac，有根据余弦定理可得
，所以可得，f（x）值域为．得到答案．解答：解：
，（Ⅰ）由
=0即
，k∈z，即对称中心的横坐标为
π，k∈z；（Ⅱ）由已知b2=ac，
，∴
∵
，∴，∴，即f（x）的值域为
，综上所述，
，f（x）值域为．点评：本题主要考查三角函数的化简和余弦定理的应用．属中档题．求三角函数值域时一定多注意自变量x的取值范围．
练习册系列答案
相关题目
cos
+
cos2
.
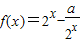（a∈R），将y=f（x）的图象向右平移两个单位，得到函数y=g（x）的图象，函数y=h（x）与函数y=g（x）的图象关于直线y=1对称．
·cos
+
cos2
.