题目内容
4.已知函数f(x)对任意的x∈R都满足f(x)+f(-x)=0,当x≥0时,f(x)=$\left\{\begin{array}{l}{-x,0≤x≤a}\\{-a,a<x<2a}\\{x-3a,x≥2a}\end{array}\right.$,(a>0),若对?x∈R,都有f(x-2)≤f(x),则实数a的取值范围为( )| A. | (0,$\frac{1}{4}$) | B. | [$\frac{1}{4}$,$\frac{1}{3}$] | C. | (0,$\frac{1}{3}$] | D. | (0,$\frac{1}{3}$) |
分析 函数f(x)对任意的x∈R都满足f(x)+f(-x)=0,可得函数f(x)是奇函数.利用奇函数的对称性画出图象.及其对?x∈R,都有f(x-2)≤f(x),即可得出.
解答 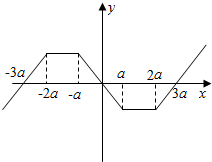 解:函数f(x)对任意的x∈R都满足f(x)+f(-x)=0,即f(-x)=-f(x),因此函数f(x)是奇函数.
解:函数f(x)对任意的x∈R都满足f(x)+f(-x)=0,即f(-x)=-f(x),因此函数f(x)是奇函数.
当x≥0时,f(x)=$\left\{\begin{array}{l}{-x,0≤x≤a}\\{-a,a<x<2a}\\{x-3a,x≥2a}\end{array}\right.$,(a>0),利用对称性画出图象.
∵对?x∈R,都有f(x-2)≤f(x),
∴将函数f(x)的图象向右平移2个单位后的图象在y=f(x)的图象的非上方,
∴6a≤2,a>0,
解得$0<a≤\frac{1}{3}$.
则实数a的取值范围是$0<a≤\frac{1}{3}$.
故选:C.
点评 本题考查了函数的奇偶性与单调性,考查了数形结合思想方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.函数y=1+logax(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny-2=0上,其中mn>0,则$\frac{1}{m}+\frac{3}{n}$的最小
值为( )
值为( )
| A. | 2+$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
16.若$\sqrt{x}+\sqrt{y}≤a\sqrt{x+y}$(x>0,y>0)恒成立,则a的最小值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
14.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x(x>0)}\\{{2}^{-x}+1(x≤0)}\end{array}\right.$,则f(f(1))+f(log2$\frac{1}{3}$)的值是( )
| A. | 6 | B. | 5 | C. | $\frac{7}{2}$ | D. | $\frac{5}{3}$ |
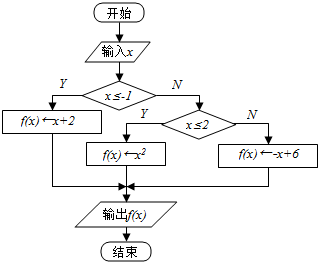 根据流程图,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是(-∞,0)∪(1,4).
根据流程图,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是(-∞,0)∪(1,4).