题目内容
14.若函数f(x)=asinx+cosx在区间$(\frac{π}{6},\frac{π}{4})$上单调递增,则实数a的取值范围是[1,+∞).分析 求函数的导数,利用函数单调性和导数之间的关系解f′(x)≥0恒成立即可.
解答 解:函数的导数f′(x)=acosx-sinx,
∵函数f(x)=asinx+cosx在区间$(\frac{π}{6},\frac{π}{4})$上单调递增,
∴f′(x)≥0在区间$(\frac{π}{6},\frac{π}{4})$上恒成立,
即f′(x)=acosx-sinx≥0,
即acosx≥sinx,
即a≥$\frac{sinx}{cosx}$=tanx
∵x∈$(\frac{π}{6},\frac{π}{4})$,
∴tan$\frac{π}{6}$<tanx<tan$\frac{π}{4}$,
即$\frac{\sqrt{3}}{3}$<tanx<1,
则a≥1,
故答案为:[1,+∞)
点评 本题主要考查函数单调性的应用,求函数的导数,利用导数法是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
9.已知tanθ=$\frac{1}{3}$,那么tan($θ+\frac{π}{4}$)等于( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
19.下列说法正确的是( )
| A. | 命题“?x∈R使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0” | |
| B. | “p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | |
| C. | “a>1”是“f(x)=logax(a>0,a≠1)在(0,+∞)上为增函数”的充要条件 | |
| D. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”,则¬p是真命题 |
4.已知函数f(x)对任意的x∈R都满足f(x)+f(-x)=0,当x≥0时,f(x)=$\left\{\begin{array}{l}{-x,0≤x≤a}\\{-a,a<x<2a}\\{x-3a,x≥2a}\end{array}\right.$,(a>0),若对?x∈R,都有f(x-2)≤f(x),则实数a的取值范围为( )
| A. | (0,$\frac{1}{4}$) | B. | [$\frac{1}{4}$,$\frac{1}{3}$] | C. | (0,$\frac{1}{3}$] | D. | (0,$\frac{1}{3}$) |
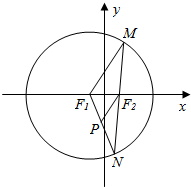 已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.
已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.