题目内容
(本题满分10分)设集合 ,
, 是
是 的两个非空子集,且满足集合
的两个非空子集,且满足集合 中的最大数小于集合
中的最大数小于集合 中的最小数,记满足条件的集合对
中的最小数,记满足条件的集合对 的个数为
的个数为 .
.
(1)求 的值;
的值;
(2)求 的表达式.
的表达式.
(Ⅰ) ,
, (Ⅱ)
(Ⅱ)
【解析】
试题分析:(Ⅰ)根据具体数值,结合新定义,列举满足条件的数对:当 时,即
时,即 ,此时
,此时 ,
, ,所以
,所以 ,当
,当 时,即
时,即 ,若
,若 ,则
,则 ,或
,或 ,或
,或 ;
;
若 或
或 ,则
,则 ;所以
;所以 .(Ⅱ)由定义知,A,B无共同元素,分别在两部分取相应子集:当集合
.(Ⅱ)由定义知,A,B无共同元素,分别在两部分取相应子集:当集合 中的最大元素为“
中的最大元素为“ ”时,集合
”时,集合 的其余元素可在
的其余元素可在 中任取若干个(包含不取),所以集合
中任取若干个(包含不取),所以集合 共有
共有 种情况,此时,集合
种情况,此时,集合 的元素只能在
的元素只能在 中任取若干个(至少取1个),所以集合
中任取若干个(至少取1个),所以集合 共有
共有 种情况,集合对
种情况,集合对 共有
共有 对,再求和
对,再求和
试题解析:(1)当 时,即
时,即 ,此时
,此时 ,
, ,所以
,所以 , 2分
, 2分
当 时,即
时,即 ,若
,若 ,则
,则 ,或
,或 ,或
,或 ;
;
若 或
或 ,则
,则 ;所以
;所以 . 4分
. 4分
(2)当集合 中的最大元素为“
中的最大元素为“ ”时,集合
”时,集合 的其余元素可在
的其余元素可在 中任取若干个(包含不取),所以集合
中任取若干个(包含不取),所以集合 共有
共有 种情况, 6分
种情况, 6分
此时,集合 的元素只能在
的元素只能在 中任取若干个(至少取1个),所以集合
中任取若干个(至少取1个),所以集合 共有
共有 种情况,
种情况,
所以,当集合 中的最大元素为“
中的最大元素为“ ”时,
”时,
集合对 共有
共有 对, 8分
对, 8分
当 依次取
依次取 时,可分别得到集合对
时,可分别得到集合对 的个数,
的个数,
求和可得 . 10分
. 10分
考点:归纳找规律

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 ( )
( ) 
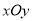 中,设直线
中,设直线 与圆
与圆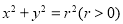 交于
交于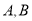 两点,
两点,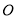 为坐标原点,若圆上一点
为坐标原点,若圆上一点 满足
满足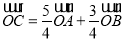 ,则
,则 .
. 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,则
的焦点重合,则 .
. 为
为 的斜边
的斜边 的延长线上一点,且
的延长线上一点,且 与
与 的外接圆相切,过点
的外接圆相切,过点 作
作 的垂线,垂足为
的垂线,垂足为 ,若
,若 ,
, ,求线段
,求线段 的长.
的长.
 满足
满足 ,
, ,
, ,若数列
,若数列 单调递减,数列
单调递减,数列 单调递增,则数列
单调递增,则数列 .
. 、
、 满足:
满足: ,
, ,
, .
. 的值;
的值; 项和
项和 的值.
的值. 是各项均为正数的等差数列,其中
是各项均为正数的等差数列,其中 ,且
,且 成等比数列;数列
成等比数列;数列 的前
的前 项和为
项和为 ,满足
,满足 .
. ,设数列
,设数列 的前
的前 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成立,若存在,求出
成立,若存在,求出