题目内容
已知双曲线的中心在坐标原点,离心率e=2,且它的一个顶点与抛物线y2=-4x的焦点重合,则此双曲线的方程为
- A.

- B.

- C.
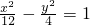
- D.
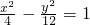
A
分析:先根据抛物线方程求得焦点坐标,进而确定双曲线的顶点,求得双曲线中的a,根据离心率进而求c,最后根据b2=c2-a2求得b,则双曲线的方程可得.
解答:由题可设双曲线的方程为: =1.
=1.
∵抛物线y2=-4x中2p=4
∴其焦点F(-1,0),
又因为双曲线的一个顶点与抛物线y2=-4x的焦点重合
则有:a=1,又e= =2
=2
∴c=2,故b2=4-1=3
双曲线的方程为 x2- =1.
=1.
故选:A.
点评:本题主要考查了双曲线的标准方程、圆锥曲线的共同特征,解答关键是对于圆锥曲线的共同特征的理解与应用.
分析:先根据抛物线方程求得焦点坐标,进而确定双曲线的顶点,求得双曲线中的a,根据离心率进而求c,最后根据b2=c2-a2求得b,则双曲线的方程可得.
解答:由题可设双曲线的方程为:
 =1.
=1.∵抛物线y2=-4x中2p=4
∴其焦点F(-1,0),
又因为双曲线的一个顶点与抛物线y2=-4x的焦点重合
则有:a=1,又e=
 =2
=2∴c=2,故b2=4-1=3
双曲线的方程为 x2-
 =1.
=1.故选:A.
点评:本题主要考查了双曲线的标准方程、圆锥曲线的共同特征,解答关键是对于圆锥曲线的共同特征的理解与应用.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 ,且前n项的算术平均数等于第n项的2n-1倍(n∈N*).
,且前n项的算术平均数等于第n项的2n-1倍(n∈N*). 高二某班要办文明礼仪的专刊,现有红、黄、白、绿、蓝五种颜色的粉笔供选用,要求在黑板中A、B、C、D每一部分只写一种颜色,如图所示,相邻两块颜色不同,则不同颜色的书写方法共有________种.
高二某班要办文明礼仪的专刊,现有红、黄、白、绿、蓝五种颜色的粉笔供选用,要求在黑板中A、B、C、D每一部分只写一种颜色,如图所示,相邻两块颜色不同,则不同颜色的书写方法共有________种. 的反函数为h(x),又函数g(x)与h(x+1)的图象关于有线y=x对称,则g(2)的值为
的反函数为h(x),又函数g(x)与h(x+1)的图象关于有线y=x对称,则g(2)的值为

 一个几何体的正视图和侧视图如图所示,则这个几何体的俯视图不可能是
一个几何体的正视图和侧视图如图所示,则这个几何体的俯视图不可能是



 如图所示,梯形A1B1C1D1是一平面图形ABCD的直观图.若A1D1∥O1y,A1B1∥C1D1,
如图所示,梯形A1B1C1D1是一平面图形ABCD的直观图.若A1D1∥O1y,A1B1∥C1D1, ,A1D1=O'D1=1.则原图形的面积为________.
,A1D1=O'D1=1.则原图形的面积为________.