题目内容
11.求值:$|\begin{array}{l}{arcsin\frac{\sqrt{3}}{2}}&{2}\\{arctan\frac{\sqrt{3}}{3}}&{3}\end{array}|$=$\frac{2π}{3}$弧度.分析 利用二阶行列式展开法则由原式得到$3arcsin\frac{\sqrt{3}}{2}$-2arctan$\frac{\sqrt{3}}{3}$,再利用反三角函数性质能求出结果.
解答 解::$|\begin{array}{l}{arcsin\frac{\sqrt{3}}{2}}&{2}\\{arctan\frac{\sqrt{3}}{3}}&{3}\end{array}|$
=$3arcsin\frac{\sqrt{3}}{2}$-2arctan$\frac{\sqrt{3}}{3}$
=3×$\frac{π}{3}$-2×$\frac{π}{6}$=$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题考查二阶行列式求值,是基础题,解题时要认真审题,注意二阶行列式展开法则的合理运用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
16.将4本完全相同的小说,1本诗集全部分给4名同学,每名同学至少1本书,则不同分法有( )
| A. | 24种 | B. | 28种 | C. | 32种 | D. | 16种 |
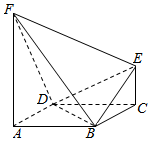 如图,在几何体ABCDEF中,FA⊥平面ABCD,EC∥FA,FA=2EC=2$\sqrt{2}$,底面ABCD为平行四边形,AD⊥BD,AD=BD=2,FD⊥BE.
如图,在几何体ABCDEF中,FA⊥平面ABCD,EC∥FA,FA=2EC=2$\sqrt{2}$,底面ABCD为平行四边形,AD⊥BD,AD=BD=2,FD⊥BE. 如图所示,四棱锥S-ABCD中,底面ABCD为正方形,且AB=4,SA⊥平面ABCD,∠SDA=60°,E、F、G分别是SC、SD、AC上的点,且$\frac{SE}{EC}$=$\frac{SF}{FD}$=$\frac{AG}{GC}$.
如图所示,四棱锥S-ABCD中,底面ABCD为正方形,且AB=4,SA⊥平面ABCD,∠SDA=60°,E、F、G分别是SC、SD、AC上的点,且$\frac{SE}{EC}$=$\frac{SF}{FD}$=$\frac{AG}{GC}$.
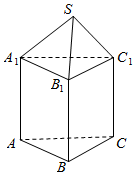 如图所示的几何体是由一个正三棱锥S-A1B1C1和一个所有棱长都相等的正三棱柱ABC-A1B1C1组合而成,且该几何体的外接球(几何体的所有顶点都在该球面上)的表面积为7π,则三棱锥S-A1B1C1的体积为$\frac{\sqrt{21}-3}{8}$.
如图所示的几何体是由一个正三棱锥S-A1B1C1和一个所有棱长都相等的正三棱柱ABC-A1B1C1组合而成,且该几何体的外接球(几何体的所有顶点都在该球面上)的表面积为7π,则三棱锥S-A1B1C1的体积为$\frac{\sqrt{21}-3}{8}$.