题目内容
12．计算：${∫}_{1}^{3}$（x-5）dx=-6．分析 根据定积分的计算法则计算即可．
解答 解：${∫}_{1}^{3}$（x-5）dx=（$\frac{1}{2}$x2-5x）|${\;}_{1}^{3}$=（$\frac{9}{2}$-15）-（$\frac{1}{2}$-5）=-6，
故答案为：-6
点评 本题考查了定积分的计算，属于基础题．
练习册系列答案
相关题目
3．已知3sin2α+2sin2β=1，3sin2α-2sin2β=0，且α、β都是锐角，则α+2β的值为（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | $\frac{π}{3}$ | D． | $\frac{π}{4}$ |
7．用数学归纳法证明等式1+3+5+…+（2n+5）=（n+3）2（n∈N*）时，验证n=1，左边应取的项是（ ）
| A． | 1 | B． | 1+3 | C． | 1+3+5 | D． | 1+3+5+7 |
17．已知函数$f（x）=\left\{\begin{array}{l}|{lnx}|\\ 2-lnx\end{array}\right.$$\begin{array}{l}0＜x≤e\\ x＞e\end{array}$，若正实数a，b，c互不相等，且f（a）=f（b）=f（c），则a•b•c的取值范围为（ ）
| A． | （e，e2） | B． | （1，e2） | C． | $（\frac{1}{e}，e）$ | D． | $（\frac{1}{e}，{e^2}）$ |
4．已知命题p：?a＞0，a+$\frac{1}{a}$≥2，命题q：?x0∈R，sinx0+cosx0=$\sqrt{3}$，则下列判断正确的是（ ）
| A． | p是假命题 | B． | q是真命题 | C． | p（∧￢q） 是真命题 | D． | （￢p）∧q是真命题 |
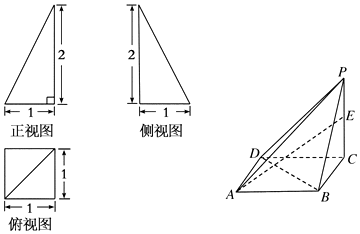
三棱锥A-BCD中，E是BC的中点，AB=AD，BD⊥DC