题目内容
13．在等差数列{an}中，如果a3=4，则a1a5的最大值为（ ）| A． | 2 | B． | 4 | C． | 8 | D． | 16 |
分析 由等差数列的性质得a1+a5=2a3=8，由此能求出a1a5的最大值．
解答 解：∵在等差数列{an}中，a3=4，
∴a1+a5=2a3=8，
∴a1a5≤（$\frac{{a}_{1}+{a}_{5}}{2}$）2=16．
当且仅当a1=a5=4时，取等号，
∴a1a5的最大值为16．
故选：D．
点评 本题考查等差数列中两项积的最大值的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
3．若tanθ=$\frac{1}{3}$，则cos2θ=（ ）
| A． | $-\frac{4}{5}$ | B． | $-\frac{1}{5}$ | C． | $\frac{1}{5}$ | D． | $\frac{4}{5}$ |
4．设a=20.3，b=0.22，c=logx（x2+0.3）（x＞1），则a，b，c的大小关系是（ ）
| A． | a＜b＜c | B． | b＜a＜c | C． | c＜b＜a | D． | b＜c＜a |
1．已知数列{an}为等比数列，且a3a13+2a82=5π，则cos（a5a11）的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | -$\frac{1}{2}$ |
8．已知命题p：?x≥4，log2x≥2；命题q：在△ABC中，若A＞$\frac{π}{3}$，则sinA＞$\frac{{\sqrt{3}}}{2}$．则下列命题为真命题的是（ ）
| A． | p∧q | B． | p∧（?q） | C． | （?p）∧（?q） | D． | （?p）∨q |
18．将函数f（x）=$\frac{1}{2}sin（{2x+φ}）$的图象向左平移$\frac{π}{6}$个单位，再将图象上各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象关于x=$\frac{π}{3}$对称，则|φ|的最小值为（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{6}$ |
5．已知A={1，3，9，27，81}，B={y|y=log3x，x∈A}，则A∩B=（ ）
| A． | {1，3} | B． | {3，27，81} | C． | {1，3，9} | D． | {9，27} |
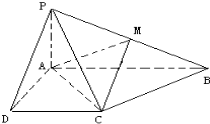如图所示，在四棱锥P-ABCD中，底面ABCD为直角梯形，AB∥CD，∠DAB=90°，PA⊥平面ABCD，且PA=CD=AD=$\frac{1}{2}$AB，M为PB的中点．