题目内容
18.将函数f(x)=$\frac{1}{2}sin({2x+φ})$的图象向左平移$\frac{π}{6}$个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象关于x=$\frac{π}{3}$对称,则|φ|的最小值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,三角函数的图象的对称性,求得|φ|的最小值.
解答 解:将函数f(x)=$\frac{1}{2}sin({2x+φ})$的图象向左平移$\frac{π}{6}$个单位,可得y=$\frac{1}{2}$sin[2(x+$\frac{π}{6}$)+φ]=$\frac{1}{2}$sin(2x+$\frac{π}{3}$+φ)的图象;
再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),可得y=$\frac{1}{2}$sin(x+$\frac{π}{3}$+φ)的图象.
根据所得图象关于x=$\frac{π}{3}$对称,可得$\frac{2π}{3}$+φ=kπ+$\frac{π}{2}$,即 φ=kπ-$\frac{π}{6}$,
故|φ|的最小值为$\frac{π}{6}$,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,三角函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
6.设函数f(x)=${e^x}({{x^3}+\frac{3}{2}{x^2}-6x+2})-2a{e^x}$-x,若不等式f(x)≤0在[-2,+∞)上有解,则实数a的最小值为( )
| A. | $-\frac{3}{2}-\frac{1}{e}$ | B. | $-\frac{3}{2}-\frac{2}{e}$ | C. | $-\frac{3}{4}-\frac{1}{2e}$ | D. | $-1-\frac{1}{e}$ |
13.在等差数列{an}中,如果a3=4,则a1a5的最大值为( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
10. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为9尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为9尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( )
 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为9尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为9尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( )| A. | 14斛 | B. | 28斛 | C. | 36斛 | D. | 66斛 |
19.某几何体是组合体,其三视图如图所示,则该几何体的体积为( )
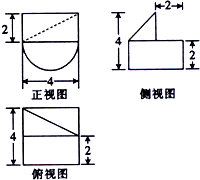

| A. | $\frac{16}{3}$+8π | B. | $\frac{32}{3}$+8π | C. | 16+8π | D. | $\frac{16}{3}$+16π |
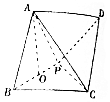 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,点A在平面PBC上的射影为PB的中点O,PB⊥AC.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,点A在平面PBC上的射影为PB的中点O,PB⊥AC.