题目内容
4.若等差数列{an}的前n项和为Sn,a4=4,S4=10,则数列$\left\{{\frac{1}{{\;{a_n}{a_{n+1}}\;}}}\right\}$的前2018项的和为$\frac{2018}{2019}$.分析 由已知列式求出等差数列的首项和公差,得到等差数列的通项公式,代入$\left\{{\frac{1}{{\;{a_n}{a_{n+1}}\;}}}\right\}$,利用裂项相消法求和.
解答 解:由a4=4,S4=10,得$\left\{\begin{array}{l}{a_4}={a_1}+3d=4\\{S_4}=4{a_1}+\frac{4×3}{2}d=10\end{array}\right.$,解得$\left\{\begin{array}{l}{a_1}=1\\ d=1\end{array}\right.$,
∴an=n,
∴$\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{{n({n+1})}}=\frac{1}{n}-\frac{1}{n+1}$,
则数列$\left\{{\frac{1}{{\;{a_n}{a_{n+1}}\;}}}\right\}$的前2018项的和为$({1-\frac{1}{2}})+({\frac{1}{2}-\frac{1}{3}})+({\frac{1}{3}-\frac{1}{4}})+…+({\frac{1}{2017}-\frac{1}{2018}})+({\frac{1}{2018}-\frac{1}{2019}})=1-\frac{1}{2019}=\frac{2018}{2019}$.
故答案为:$\frac{2018}{2019}$.
点评 本题考查裂项相消法求数列的前n项和,考查等差数列通项公式的求法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.四个平面互不平行,也不重合,则它们的交线数不可能是( )
| A. | 1条 | B. | 2条 | C. | 4条 | D. | 6条 |
16.函数$f(x)=sin(2x+θ)+\sqrt{3}cos(2x+θ)$为奇函数,且在$[-\frac{π}{4},0]$上为减函数的θ值可以是( )
| A. | $-\frac{π}{3}$ | B. | $-\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
14.定义2×2矩阵$[\begin{array}{l}{a_1}\\{a_3}\end{array}\right.\left.\begin{array}{l}{a_2}\\{a_4}\end{array}]={a_1}{a_4}-{a_2}{a_3}$,若$f(x)=[{\begin{array}{l}{cosx-sinx}&{\sqrt{3}}\\{cos(\frac{π}{2}+2x)}&{cosx+sinx}\end{array}}]$,则f(x)( )
| A. | .图象关于(π,0)中心对称 | B. | 图象关于直线$x=\frac{π}{2}$对称 | ||
| C. | 在区间$[-\frac{π}{6},0]$上单调递增 | D. | 周期为π的奇函数 |
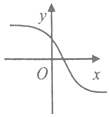
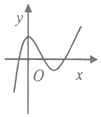
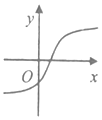
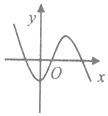
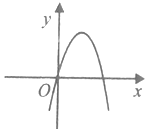 已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )
已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )