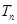题目内容
(满分12分)设数列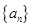 的前
的前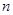 项和为
项和为 .已知
.已知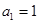 ,
, ,
,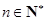 。
。
(Ⅰ)求数列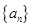 的通项公式;
的通项公式;
(Ⅱ)记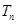 为数列
为数列 的前
的前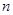 项和,求
项和,求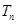 ;
;
(Ⅰ)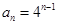 (
(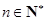 ). (Ⅱ)
). (Ⅱ)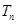
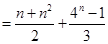
解析试题分析:(Ⅰ)由题意, ,则当
,则当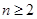 时,
时,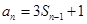 .
.
两式相减,得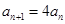 (
(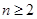 ).
).
又因为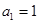 ,
,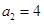 ,
,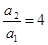 ,
,
所以数列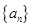 是以首项为
是以首项为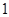 ,公比为
,公比为 的等比数列,
的等比数列,
所以数列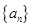 的通项公式是
的通项公式是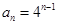 (
(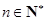 ).
).
(Ⅱ)因为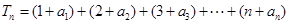 ,
,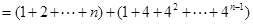
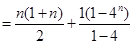
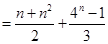
考点:本题主要考查等比数列的通项公式、求和公式,等差数列的求和。
点评:基础题,等比数列、等差数列相关内容,已是高考必考内容,其难度飘忽不定,有时突出考查求和问题,如“分组求和法”、“裂项相消法”、“错位相减法”等,有时则突出涉及数列的证明题。本题解法中,注意通过研究 ,确定得到数列的通项公式,带有普遍性。
,确定得到数列的通项公式,带有普遍性。

练习册系列答案
相关题目
已知数列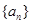 满足
满足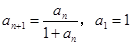 ,归纳出
,归纳出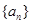 的一个通项公式为( )
的一个通项公式为( )
A.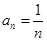 | B.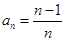 | C.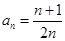 | D.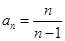 |
 中,
中,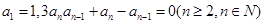
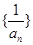 是否为等差数列;
是否为等差数列;
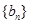 满足
满足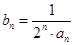 ,求数列
,求数列 ;
;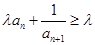 ,对任意n ≥2的整数恒成立,求实数
,对任意n ≥2的整数恒成立,求实数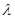 的取值范围.
的取值范围.
 行里的最后一个数字是多少?
行里的最后一个数字是多少?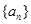 满足:
满足: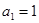 ,
,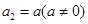 ,
,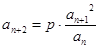 (其中
(其中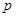 为非零常数,
为非零常数,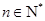 ).
). 是不是等比数列?
是不是等比数列?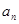 ;
;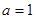 时,令
时,令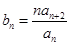 ,
,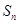 为数列
为数列 的前
的前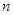 项和,求
项和,求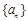 满足:
满足: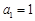 ,
,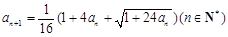 。
。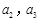 ;
; 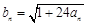 ,求数列
,求数列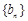 的通项公式;
的通项公式;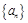 中的各项均为正数,且满足
中的各项均为正数,且满足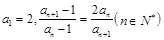 .记
.记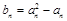 ,数列
,数列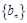 的前
的前 项和为
项和为 ,且
,且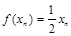 .
. 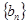 是等比数列;
是等比数列;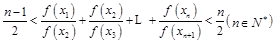 .
.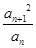 (其中P为非零常数,n∈N *)
(其中P为非零常数,n∈N *)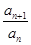 }是不是等比数列?
}是不是等比数列?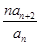 ,Sn为数列{bn}的前n项和,求Sn。
,Sn为数列{bn}的前n项和,求Sn。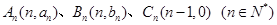 ,满足向量
,满足向量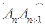 与向量
与向量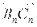 共线,且点
共线,且点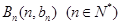 都在斜率为6的同一条直线上。若
都在斜率为6的同一条直线上。若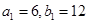 。求(1)数列
。求(1)数列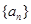 的通项
的通项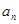 (2)数列{
(2)数列{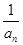 }的前n项和
}的前n项和