题目内容
已知数列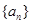 满足
满足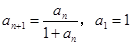 ,归纳出
,归纳出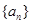 的一个通项公式为( )
的一个通项公式为( )
A.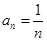 | B.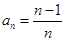 | C.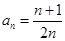 | D.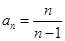 |
A
解析试题分析:由递推公式 ,可得
,可得 ,
, ,
, ,故可猜测
,故可猜测 的一个通项公式为
的一个通项公式为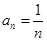 .
.
考点:归纳推理.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
数列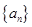 满足
满足 ,且
,且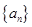 是递增数列,则实数
是递增数列,则实数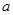 的取值范围是( )
的取值范围是( )
A. | B. | C.(1,3) | D.(2,3) |
在数列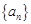 中,若对任意的
中,若对任意的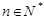 均有
均有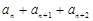 为定值,且
为定值,且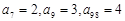 ,则数列
,则数列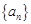 的前100项的和
的前100项的和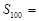 ( )
( )
| A.132 | B.299 | C.68 | D.99 |
已知数列 满足
满足 ,若
,若 ,则
,则 =( )
=( )
A.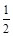 | B.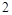 | C. | D. |
数列 满足
满足 (
( ), 那么
), 那么 的值为( )
的值为( )
| A.4 | B.8 | C.31 | D.15 |
数列 满足
满足 ,其中
,其中 ,设
,设 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
设数列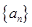 满足
满足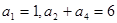 ,且对任意
,且对任意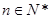 ,函数
,函数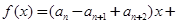
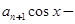
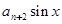 满足
满足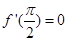 ,若
,若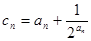 ,则数列
,则数列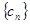 的前
的前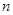 项和
项和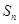 为( )
为( )
A.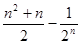 | B.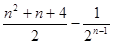 |
C.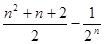 | D. |
已知数列{ }满足
}满足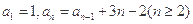 ,则
,则 的通项公式为( )
的通项公式为( )
A.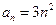 |
B. |
C.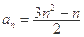 |
D.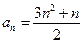 |
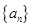 的前
的前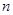 项和为
项和为 .已知
.已知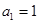 ,
, ,
,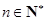 。
。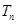 为数列
为数列 的前
的前