题目内容
已知数列{an}满足:a1=1,a2=(a≠0),an+2=p·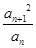 (其中P为非零常数,n∈N *)
(其中P为非零常数,n∈N *)
(1)判断数列{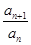 }是不是等比数列?
}是不是等比数列?
(2)求an;
(3)当a=1时,令bn=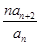 ,Sn为数列{bn}的前n项和,求Sn。
,Sn为数列{bn}的前n项和,求Sn。
(1) 数列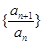 是等比数列.(2)
是等比数列.(2)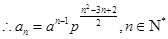 。(3)
。(3)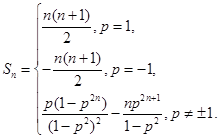 。
。
解析试题分析:(1)由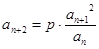 ,得
,得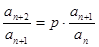 . 1分
. 1分
令 ,则
,则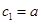 ,
,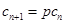 .
.
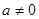 ,
,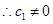 ,
, (非零常数),
(非零常数), 数列
数列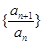 是等比数列. 3分
是等比数列. 3分
(2) 数列
数列 是首项为
是首项为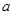 ,公比为
,公比为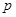 的等比数列,
的等比数列, 
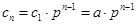 ,即
,即 . 4分
. 4分
当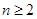 时,
时,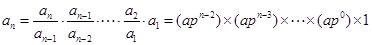
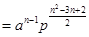 , 6分
, 6分
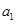 满足上式,
满足上式, 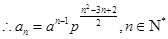 . 7分
. 7分
(3)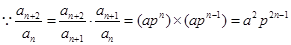 ,
, 当
当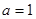 时,
时,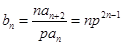 . 8分
. 8分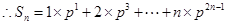 , ①
, ①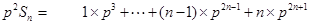 ②
② 当
当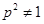 ,即
,即 时,①
时,①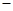 ②得:
②得: ,
,
即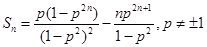 . 11分
. 11分
而当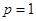 时,
时,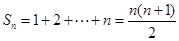 , 12分
, 12分
当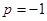 时,
时, .13分
.13分
综上所述, 14分
14分
考点:等比数列的通项公式;等比数列的前n项和公式;数列通项公式的求法;数列前n项和的求法;累乘法;错位相减法;
点评:(1)本题主要考查了等比数列的通项公式、等比数列求和公式、简单递推数列求通项、错位求和等知识,考查了学生的运算能力,以及化归与转化、分类讨论的思想.(2)利用错位相减法求和时,转化为等比数列求和,若公比是个参数(字母),则应先对参数加以讨论,一般情况下,分为等于1和不等于1两种情况分别求和。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
数列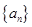 满足
满足 ,且
,且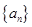 是递增数列,则实数
是递增数列,则实数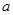 的取值范围是( )
的取值范围是( )
A. | B. | C.(1,3) | D.(2,3) |
数列 满足
满足 ,其中
,其中 ,设
,设 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
 满足
满足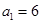 ,
,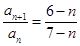
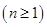 ;
;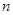 项和
项和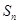 ,并求当
,并求当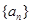 的前
的前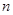 项和为
项和为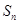 ,且有
,且有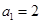 ,
,
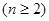 .
.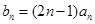 ,求数列
,求数列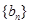 的前
的前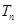 ;
;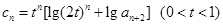 ,且数列
,且数列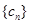 中的 每一项总小于它后面的项,求实数
中的 每一项总小于它后面的项,求实数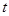 的取值范围.
的取值范围.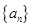 的前
的前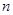 项和为
项和为 .已知
.已知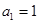 ,
, ,
,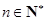 。
。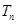 为数列
为数列 的前
的前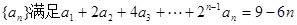 .
.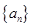 的通项公式;
的通项公式;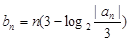 ,探求使
,探求使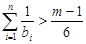 恒成立的
恒成立的 的最大整数值.
的最大整数值.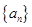 是首项为23,公差为整数的等差数列,且
是首项为23,公差为整数的等差数列,且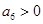 ,
,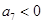 .
. 项和
项和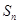 的最大值;
的最大值;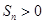 时,求
时,求