题目内容
13.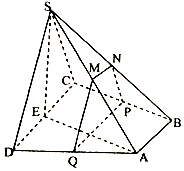 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$.
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$.(1)当t=$\frac{1}{2}$时,求证:平面SAE⊥平面MNPQ;
(2)是否存在实数t,使得二面角M-PQ-A的平面角的余弦值为$\frac{\sqrt{5}}{5}$?若存在,求出实数t的值;若不存在,说明理由.
分析 (1)推导出AE⊥CD,PQ⊥AE,从而SE⊥面ABCD,由此能证明面MNPQ⊥面SAE.
(2)以E为原点,ED,EA,ES直线分别为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出t的值.
解答 (本小题满分12分)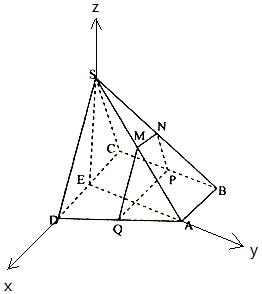
证明:(1)E为CD中点,∴四边形ABCE为矩形,
∴AE⊥CD,
当t=$\frac{1}{2}$时,Q为AD中点,PQ∥CD,所以PQ⊥AE,
∵平面SCD⊥平面ABCD,SE⊥CD,∴SE⊥面ABCD,
∵PQ?面ABCD,∴PQ⊥SE,∴PQ⊥面SAE,
所以面MNPQ⊥面SAE.
(2)如图,以E为原点,ED,EA,ES直线分别为x轴,y轴,z轴建立如图所示坐标系;
设ED=a,则M((1-t)a,($\sqrt{3}t$-$\frac{\sqrt{3}}{2}$)a,$\frac{\sqrt{3}}{2}$a),E(0,0,0),A(0,$\sqrt{3}$,0),
Q((1-t)a,$\sqrt{3}ta$,0),$\overrightarrow{MQ}$=(0,$\frac{\sqrt{3}}{2}a$,$\frac{\sqrt{3}}{2}a$),
面ABCD一个方向向量为$\overrightarrow{m}$=(1,0,0),
设平面MPQ的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{MQ}=(1-t)ax+(\sqrt{3}t-\frac{\sqrt{3}}{2})ay+\frac{\sqrt{3}}{2}az=0}\\{\overrightarrow{n}•\overrightarrow{m}=x=0}\end{array}\right.$,取z=2,得$\overrightarrow{n}$=(0,$\frac{1}{t-\frac{1}{2}}$,2),
平面ABCD的法向量为$\overrightarrow{p}$=(0,0,1)
∵二面角M-PQ-A的平面角的余弦值为$\frac{\sqrt{5}}{5}$,
∴由题意:cosθ=$\frac{|\overrightarrow{n}•\overrightarrow{p}|}{|\overrightarrow{n}|•|\overrightarrow{p}|}$=$\frac{2}{\sqrt{(\frac{1}{t-\frac{1}{2}})^{2}+4}}$=$\frac{\sqrt{5}}{5}$,
解得t=$\frac{1}{4}$或t=$\frac{3}{4}$,
由图形知,当t=$\frac{3}{4}$时,二面角M-PQ-A为钝二面角,不合题意,舍去
综上:t=$\frac{1}{4}$.
点评 本题考查面面垂直的证明,考查实数值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

(1)求φ的值;
(2)若对?x≥0,f(x)≤0恒成立,求a的取值范围;
(3)利用如表数据证明:$\sum_{k=1}^{157}{sin\frac{kπ}{314}<106}$.
| ${e^{\frac{π}{314}}}$ | ${e^{-\frac{π}{314}}}$ | ${e^{\frac{78π}{314}}}$ | ${e^{-\frac{78π}{314}}}$ | ${e^{\frac{79π}{314}}}$ | ${e^{-\frac{79π}{314}}}$ |
| 1.010 | 0.990 | 2.182 | 0.458 | 2.204 | 0.454 |
| A. | 24 | B. | 36 | C. | 16 | D. | 18 |
| A. | $[kπ-\frac{π}{3},kπ+\frac{π}{6}](k∈z)$ | B. | $[kπ-\frac{π}{6},kπ+\frac{π}{3}](k∈Z)$ | ||
| C. | $[kπ-\frac{π}{12},kπ+\frac{5π}{12}](k∈Z)$ | D. | $[kπ-\frac{5π}{12},kπ+\frac{π}{12}](k∈z)$ |