题目内容
1.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{5-x},x≤0}\\{lo{g}_{4}x,x>0}\end{array}\right.$,则f[f(-3)]=-$\frac{3}{2}$.分析 由已知得f(-3)=$\frac{1}{5-(-3)}$=$\frac{1}{8}$,从而f[f(-3)]=f($\frac{1}{8}$),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{\frac{1}{5-x},x≤0}\\{lo{g}_{4}x,x>0}\end{array}\right.$,
∴f(-3)=$\frac{1}{5-(-3)}$=$\frac{1}{8}$,
f[f(-3)]=f($\frac{1}{8}$)=$lo{{g}_{4}\frac{1}{8}}^{\;}$=$\frac{lg\frac{1}{8}}{lg4}$=$\frac{-3lg2}{2lg2}$=-$\frac{3}{2}$.
故答案为:$-\frac{3}{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
12.在△ABC中,tanC=2,BC边上的高为AD,D为垂足,且BD=2DC,则cosA=( )
| A. | $\frac{3}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{10}}{10}$ |
9.已知集合A={0,1,2},B={1,m},若A∩B=B,则实数m的取值集合是( )
| A. | {0} | B. | {2} | C. | {0,2} | D. | {0,1,2} |
16.已知命题p与命题q,若命题:(¬p)∨q为假命题则下列说法正确是( )
| A. | p真,q真 | B. | p假,q真 | C. | p真,q假 | D. | p假,q假 |
6.如图是f(x)=$\frac{{2\sqrt{3}}}{3}$cos(ωx+φ)(ω>0)的部分图象,下列说法错误的是( )
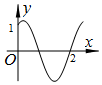
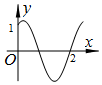
| A. | 函数f(x)的最小正周期是$\frac{12}{5}$ | |
| B. | 函数g(x)=$\frac{{2\sqrt{3}}}{3}sin\frac{5π}{6}$x的图象可由函数f(x)的图象向右平移$\frac{2}{5}$个单位得到 | |
| C. | 函数f(x)图象的一个对称中心是(-$\frac{4}{5}$,0) | |
| D. | 函数f(x)的一个递减区间是(5,$\frac{31}{5}$) |
10.已知向量$\overrightarrow{AB}$、$\overrightarrow{AC}$、$\overrightarrow{AD}$满足$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,E、F分别是线段BC、CD的中点,若$\overrightarrow{DE}$•$\overrightarrow{BF}$=-$\frac{5}{4}$,则向量$\overrightarrow{AB}$与$\overrightarrow{AD}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
11.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F(-c,0)(c>0),作倾斜角为$\frac{π}{6}$的直线FE交该双曲线右支于点P,若$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{OF}$+$\overrightarrow{OP}$),且$\overrightarrow{OE}$•$\overrightarrow{EF}$=0,则双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{5}$ | B. | $\sqrt{3}$+1 | C. | $\frac{\sqrt{10}}{2}$ | D. | $\sqrt{5}$+1 |
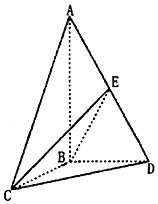 如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.
如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.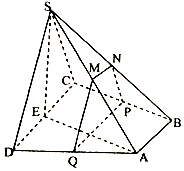 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$.
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若$\overrightarrow{DQ}$=t$\overrightarrow{DA}$.