题目内容
下列函数中，导函数是奇函数的是（ ）
| A、y=sinx | ||
| B、y=ex | ||
| C、y=lnx | ||
D、y=cosx-
|
考点：导数的运算,函数单调性的判断与证明
专题：函数的性质及应用,导数的概念及应用
分析：求出函数的导数，根据函数的奇偶性的定义进行判断即可得到结论．
解答：
解：A．函数的导数为y′=cosx，为偶函数，不满足条件．
B．函数的导数为y′=ex，为非奇非偶函数，不满足条件．
C．函数的导数为y′=
，x＞0为非奇非偶函数，不满足条件．
D．函数的导数为y′=-sinx，为奇函数，满足条件．
故选：D
B．函数的导数为y′=ex，为非奇非偶函数，不满足条件．
C．函数的导数为y′=
| 1 |
| x |
D．函数的导数为y′=-sinx，为奇函数，满足条件．
故选：D
点评：本题主要考查函数的导数计算，以及函数奇偶性的判断，根据定义是解决本题的关键，比较基础．
练习册系列答案
相关题目
（1-ax+by）n展开式中不含x的项的系数绝对值的和为243，不含y的项的系数绝对值的和为32，则a，b，n的值可能为（ ）
| A、a=2，b=-1，n=5 |
| B、a=-1，b=2，n=6 |
| C、a=-1，b=2，n=5 |
| D、a=-2，b=-1，n=6 |
若a＜b＜0，则下列不等式中成立的是（ ）
A、
| ||||
B、b+
| ||||
C、a+
| ||||
D、
|
不等式（x-2）（x-1）＜0的解集是（ ）
| A、{x|1＜x＜2} |
| B、{x|x＜1或x＞2} |
| C、{x|x＜1} |
| D、{x|x＞2} |
极坐标系中，过点（2，
）且与极轴垂直的直线方程为（ ）
| π |
| 3 |
A、ρsinθ=-
| ||
B、ρ=-
| ||
| C、ρ=-4cosθ | ||
| D、ρcosθ-1=0 |
已知点A（0，-3），B（2，3），直线x+4y-1=0过抛物线y=ax2的焦点，动点P在抛物线上，则△PAB面积的最小值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
曲线y=x3+x-2上点P0处的切线斜率为4，则点P0的一个坐标是（ ）
| A、（0，-2） |
| B、（1，1） |
| C、（-1，-4） |
| D、（1，4） |
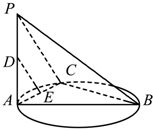如图，已知AB是圆的直径，PA垂直圆所在的平面，C是圆上任一点，D是线段PA的中点，E是线段AC上的一点．