题目内容
1．在△ABC中，内角A、B、C的对边分别为a、b、c，已知$\frac{{4\sqrt{3}}}{3}{S_{△ABC}}={b^2}+{c^2}-{a^2}$，则角A=$\frac{π}{3}$（用弧度制表示）．分析 利用三角形面积公式，余弦定理，同角三角函数基本关系式化简已知等式可得tanA=$\sqrt{3}$，结合范围A∈（0，π），可求A的值．
解答 解：∵$\frac{{4\sqrt{3}}}{3}{S_{△ABC}}={b^2}+{c^2}-{a^2}$，
∴$\frac{4\sqrt{3}}{3}$×$\frac{1}{2}$bcsinA=2bccosA，
∴$\frac{\sqrt{3}}{3}$sinA=cosA，可得：tanA=$\sqrt{3}$，
∵A∈（0，π），
∴A=$\frac{π}{3}$．
故答案为：$\frac{π}{3}$．
点评 本题主要考查了三角形面积公式，余弦定理，同角三角函数基本关系式在解三角形中应用，属于基础题．
练习册系列答案
相关题目
4．已知实数 $a={log_2}3{，^{\;}}b=\int_1^2{（{x+\frac{1}{x}}）}dx{，^{\;}}c={log_{\frac{1}{3}}}\frac{1}{30}$，则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | a＞c＞b | C． | c＞a＞b | D． | c＞b＞a |
12．（x2+xy+2y）5的展开式中x6y2的系数为（ ）
| A． | 20 | B． | 40 | C． | 60 | D． | 80 |
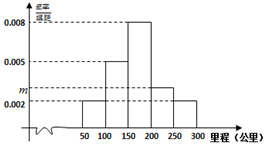绿色出行越来越受到社会的关注，越来越多的消费者对新能源汽车感兴趣．但是消费者比较关心的问题是汽车的续驶里程．某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：[50，100），[100，150），[150，200），[200，250），[250，300]，绘制成如图所示的频率分布直方图．
16．公差不为0的等差数列{an}的前n项和为Sn，若a6=3a4，且S10=λa4，则λ的值为（ ）
| A． | 15 | B． | 21 | C． | 23 | D． | 25 |
6．设全集U=R，集合A={x|x≤-2或x≥3}，B={x|x＞1}，则（∁UA）∪B=（ ）
| A． | {x|x≥-2} | B． | {x|x＞-2} | C． | {x|1＜x＜3} | D． | {x|1＜x≤3} |
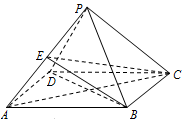已知四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°，AB=PB=PD=2，$PA=\sqrt{6}$．