题目内容
16.在Rt△ABC中,∠C=90°,AC=4,BC=2,D是BC的中点,E是AB的中点,P是△ABC(包括边界)内任一点,则$\overrightarrow{AD}$•$\overrightarrow{EP}$的取值范围是[-9,9].分析 以CA所在的直线为x轴,CB所在的直线为y轴建立平面直角坐标系,可求得$\overrightarrow{AD}$•$\overrightarrow{EP}$=-4(x-2)+(y-1),令t=-4(x-2)+(y-1),则y=4x+t-7,利用线性规划即可求得$\overrightarrow{AD}$•$\overrightarrow{EP}$的取值范围.
解答 解:以CA所在的直线为x轴,CB所在的直线为y轴建立平面直角坐标系,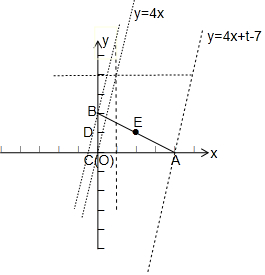
则A(4,0)、B(0,2)、D(0,1)、E(2,1),
又P是△ABC(包括边界)内任一点,设P(x,y),
则$\overrightarrow{AD}$=(-4,1),$\overrightarrow{EP}$=(x-2,y-1),$\overrightarrow{AD}$•$\overrightarrow{EP}$=-4(x-2)+(y-1),
令t=-4(x-2)+(y-1),则y=4x+t-7,
由图知,当直线y=4x+t-7过B(0,2)时,在y轴的截矩最大,此时t=2+7=9;
当直线y=4x+t-7过A(4,0)时,在y轴的截矩最小,此时t=-16+7=-9;
所以,$\overrightarrow{AD}$•$\overrightarrow{EP}$的取值范围是[-9,9],
故答案为:[-9,9].
点评 本题考查平面向量数量积的坐标运算,将$\overrightarrow{AD}$•$\overrightarrow{EP}$=-4(x-2)+(y-1),转化为:令t=-4(x-2)+(y-1),即y=4x+t-7,利用线性规划解决问题是关键,考查数形结合思想与等价转化思想的综合运用,属于难题.

练习册系列答案
相关题目
7.若复数z=1+i,$\overline z$为z的共轭复数,则z•$\overline z$=( )
| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | 2i |
4.已知函数$f(x)=sin\frac{πx}{6}$,集合M={0,1,2,3,4,5,6,7,8},现从M中任取两个不同元素m,n,则f(m)f(n)=0的概率为( )
| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{7}{18}$ | D. | $\frac{7}{9}$ |
11.若i为虚数单位,则$\frac{1+i}{3-i}$-$\frac{i}{3+i}$=( )
| A. | $\frac{2-i}{10}$ | B. | $\frac{1+i}{10}$ | C. | $\frac{4+7i}{10}$ | D. | $\frac{4-i}{10}$ |
1.A={a|f(x)=$\frac{1}{\sqrt{a{x}^{2}+3ax+1}}$的定义域为R},B={a|3a2+5a-2<0},则A∩B=( )
| A. | (0,$\frac{4}{9}$) | B. | [0,$\frac{1}{3}$) | C. | (-2,0) | D. | ($\frac{1}{3}$,$\frac{4}{9}$) |
18.证明$\frac{n+2}{2}<1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+…+\frac{1}{2^n}<n+1(n>1)$,当n=2时,中间式子等于( )
| A. | 1 | B. | $1+\frac{1}{2}$ | C. | $1+\frac{1}{2}+\frac{1}{3}$ | D. | $1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ |
19.函数$f(x)={e^2}x+\frac{1}{x},g(x)=\frac{ex}{{{e^{x-1}}}}$,对任意x1,x2∈(0,+∞),不等式(k+1)g(x1)≤kf(x2)(k>0)恒成立,则实数k的取值范围是( )
| A. | [1,+∞) | B. | (2,+∞] | C. | (0,2) | D. | (0,1] |