题目内容
19.函数$f(x)={e^2}x+\frac{1}{x},g(x)=\frac{ex}{{{e^{x-1}}}}$,对任意x1,x2∈(0,+∞),不等式(k+1)g(x1)≤kf(x2)(k>0)恒成立,则实数k的取值范围是( )| A. | [1,+∞) | B. | (2,+∞] | C. | (0,2) | D. | (0,1] |
分析 利用基本不等式可求f(x)的最小值,对函数g(x)求导,利用导数研究函数的单调性,进而可求g(x)的最大值,f(x)的最小值,得到关于k的不等式,解出即可.
解答 解:∵当x>0时,f(x)=e2x+$\frac{1}{x}$≥2 $\sqrt{{e}^{2}x•\frac{1}{x}}$=2e,
∴x1∈(0,+∞)时,函数f(x2)有最小值2e,
∵g(x)=$\frac{ex}{{e}^{x-1}}$,∴g′(x)=$\frac{{e}^{2}(1-x)}{{e}^{x}}$,
当x<1时,g′(x)>0,则函数g(x)在(0,1)上单调递增,
当x>1时,g′(x)<0,则函数在(1,+∞)上单调递减,
∴x=1时,函数g(x)有最大值g(1)=e,
则有x1、x2∈(0,+∞),f(x2)min=2e>g(x1)max=e
∵(k+1)g(x1)≤kf(x2)(k>0),
∴$\frac{g{(x}_{1})}{k}$≤$\frac{f{(x}_{2})}{k+1}$恒成立且k>0,$\frac{e}{k}$≤$\frac{2e}{k+1}$,
∴k≥1
故选:A.
点评 本题主要考查了利用基本不等式求解函数的最值,导数在函数的单调性,最值求解中的应用是解答本题的另一重要方法,函数的恒成立问题的转化,本题具有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.如果|cos θ|=$\frac{1}{5}$,$\frac{7π}{2}$<θ<4π,那么cos$\frac{θ}{2}$的值等于( )
| A. | $\frac{\sqrt{10}}{5}$ | B. | -$\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{15}}{5}$ | D. | -$\frac{\sqrt{15}}{5}$ |
4.函数$f(x)=2sin({ωx+φ})({0<ω<12,|φ|<\frac{π}{2}})$,若$f(0)=-\sqrt{3}$,且函数f(x)的图象关于直线$x=-\frac{π}{12}$对称,则以下结论正确的是( )
| A. | 函数f(x)的最小正周期为$\frac{π}{3}$ | |
| B. | 函数f(x)的图象关于点$({\frac{7π}{9},0})$对称 | |
| C. | 函数f(x)在区间$({\frac{π}{4},\frac{11π}{24}})$上是增函数 | |
| D. | 由y=2cos2x的图象向右平移$\frac{5π}{12}$个单位长度可以得到函数f(x)的图象 |
11.设f(x)是定义在R上周期为2的奇函数,当0≤x≤1时,f(x)=x2-x,则$f({-\frac{5}{2}})$=( )
| A. | $-\frac{1}{4}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
 设椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的长轴长为6,离心率$e=\frac{{\sqrt{6}}}{3}$,O为坐标原点.
设椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的长轴长为6,离心率$e=\frac{{\sqrt{6}}}{3}$,O为坐标原点.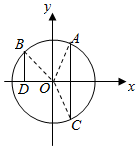 (理) 如图,在平面直角坐标系xoy中,点A(x1,y1),B(x2,y2)在单位圆上,∠xOA=α,$α∈(\frac{π}{6},\frac{π}{2})$,$∠AOB=\frac{π}{3}$.
(理) 如图,在平面直角坐标系xoy中,点A(x1,y1),B(x2,y2)在单位圆上,∠xOA=α,$α∈(\frac{π}{6},\frac{π}{2})$,$∠AOB=\frac{π}{3}$.