题目内容
已知点P是曲线C：
（θ为参数，π≤θ≤2π）上一点，O为原点．若直线OP的倾斜角为
，求点P的直角坐标．
|
| π |
| 3 |
考点：参数方程化成普通方程
专题：计算题,坐标系和参数方程
分析：将参数方程化为普通方程，注意y≤0，联立方程，求出点P的坐标，注意取舍．
解答：
解：由题意得，曲线C的直角坐标方程为
+
=1(y≤0)，
直线OP方程为y=
x，
方程联立得，
（舍去），或
，
故点P的直角坐标为（-
，-
）．
| x2 |
| 4 |
| y2 |
| 3 |
直线OP方程为y=
| 3 |
方程联立得，
|
|
故点P的直角坐标为（-
2
| ||
| 5 |
2
| ||
| 5 |
点评：本题主要考查参数方程与直角坐标方程的互化，注意参数的范围，属于基础题．
练习册系列答案
相关题目
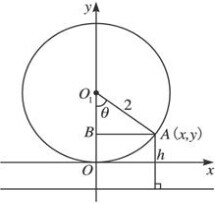如图，某大风车的半径为2米，每12秒旋转一周，它的最低点O离地面0.5米．风车圆周上一点A从最低点O开始，运动t秒后与地面的距离为h米．以O为原点，过点O的圆的切线为x轴，建立直角坐标系．