若10m=2.10n=4.则${10}^{\frac{3m-2n}{2}}$=$\frac{\sqrt{2}}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

16．若10^m=2，10ⁿ=4，则${10}^{\frac{3m-2n}{2}}$=$\frac{\sqrt{2}}{2}$．

分析根据指数幂的运算性质计算即可．

解答解：∵10^m=2，10ⁿ=4，
∴$1{0}^{\frac{3m-2n}{2}}$=$\sqrt{1{0}^{3m-2n}}$=$\sqrt{（1{0}^{m}）^{3}÷（1{0}^{n}）^{2}}$=$\sqrt{{2}^{3}÷{4}^{2}}$=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$，
故答案为：$\frac{\sqrt{2}}{2}$．

点评本题考查了指数幂的运算性质，属于基础题．

练习册系列答案

7．对于?x∈R，等式x⁵=a₀+a₁（x-2）+a₂（x-2）²+A+a₅（x-2）⁵恒成立，则a₂=80．

4．

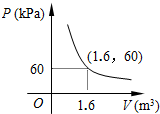某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P （ kPa ）是气体体积V （ m³）的反比例函数，其图象如图所示．当气球内的气压大于120kPa时，气球将爆炸．为了安全起见，气球的体积应（　　）

11．四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{DC}$=（1，1），$\frac{1}{|\overrightarrow{BA}|}$$\overrightarrow{BA}$+$\frac{1}{|\overrightarrow{BC}|}$$\overrightarrow{BC}$=$\frac{\sqrt{3}}{|\overrightarrow{BD}|}$$\overrightarrow{BD}$，则四边形ABCD的面积是$\sqrt{3}$．

1．已知方程4x²+2（m-1）x+（2m+3）=0（m∈R）有两个负根，求m的取值范围．

8．一种放射性物质不断变化为其他物质，每经过一年剩留的质量约是原来的84%，估计约经过多少年，该物质的剩留量是原来的一半．（结果保留1个有效数字）

5．集合M={x|log₂（x²-3x+2）＜1}，N={x|x＜a}，若M⊆N，则a的取值范围是（　　）

6．已知函数f（x）=alog₂x-blog₃x+3，若f（$\frac{1}{2015}$）=5，则f（2015）等于（　　）

试题分类