题目内容
18.设数列{an}的前n项和为Sn,并且满足2Sn=an2+n,an>0.猜想{an}的通项公式,并用数学归纳法加以证明.分析 由2Sn=an2+n,an>0.n=1时,2a1=${a}_{1}^{2}$+1,解得a1=1.同理可得a2=2,….猜想an=n.再利用数学归纳法证明即可.
解答 解:由2Sn=an2+n,an>0.n=1时,2a1=${a}_{1}^{2}$+1,解得a1=1.
n=2时,2(1+a2)=${a}_{2}^{2}$+2,解得a2=2,….
猜想an=n.
下面利用数学归纳法证明:(1)当n=1时,a1=1成立.
(2)假设n=k∈N*时,ak=k.则Sk=$\frac{k(k+1)}{2}$.
则n=k+1时,2$[\frac{k(k+1)}{2}+{a}_{k+1}]$=${a}_{k+1}^{2}$+k+1,ak+1>0,解得ak+1=k+1.
∴n=k+1时有时成立.
综上可得:an=n对?n∈N*都成立.
点评 本题考查了数列递推关系、猜想方法、数学归纳法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知函数$f(x)=\left\{\begin{array}{l}a•{2^x},x≥0\\{2^{-x}},x<0\end{array}\right.$(a∈R),若f(f(-1))=1,则a=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
3.设曲线$\left\{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}\right.$与x轴交点为M、N,点P在曲线上,则PM与PN所在直线的斜率之积为( )
| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
8.阅读下面的程序框图,运行相应的程序,则输出的K和S的值分别为( )
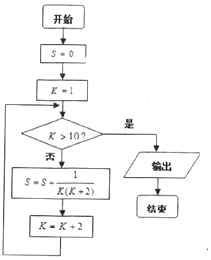

| A. | 9,$\frac{4}{9}$ | B. | 11,$\frac{5}{11}$ | C. | 11,$\frac{10}{11}$ | D. | 13,$\frac{12}{13}$ |
 ,其中A的各位数字中,a1=1,且ak(k=2,3,4,5)为0和1的概率分别是$\frac{1}{4}$和$\frac{3}{4}$.记ξ=a1+a2+a3+a4+a5,当程序运行一次时:
,其中A的各位数字中,a1=1,且ak(k=2,3,4,5)为0和1的概率分别是$\frac{1}{4}$和$\frac{3}{4}$.记ξ=a1+a2+a3+a4+a5,当程序运行一次时: