题目内容
已知定义在(0,+∞)上的函数f(x)=x2+
(a>0)的最小值为3.
(Ⅰ)求a的值;
(Ⅱ)求不等式|x-a|+|x+1|≤4的解集.
| a |
| x |
(Ⅰ)求a的值;
(Ⅱ)求不等式|x-a|+|x+1|≤4的解集.
考点:绝对值不等式的解法,基本不等式
专题:不等式
分析:(Ⅰ)因为a>0,x>0,得到x2+
≥3
=3
,当且仅当x2=
,即x=
时等号成立,从而求出a的值;
(Ⅱ)原不等式等价于
或
或
,解出即可.
| a |
| x |
| 3 | x2•
| ||||
| 3 |
| ||
| a |
| 2x |
| 3 |
| ||
(Ⅱ)原不等式等价于
|
|
|
解答:
解:(Ⅰ)因为a>0,x>0,根据三个正数的算术-几何平均不等式,得
f(x)=x2+
=x2+
+
≥3
=3
,当且仅当x2=
,即x=
时等号成立,
又因为函数f(x)的最小值为3,所以3
=3,(a>0),
解得:a=2.
(Ⅱ)解法一:由(Ⅰ)得:|x-2|+|x+1|≤4.
原不等式等价于
或
或
,
解得-
≤x≤
.所以原不等式解集为{x|-
≤x≤
}.
解法二:由(Ⅰ)得:|x-2|+|x+1|≤4.
由绝对值的几何意义,可知该不等式即求数轴上到点2和点-1的距离之和不大于4的点的集合.
故原不等式解集为{x|-
≤x≤
}.
f(x)=x2+
| a |
| x |
| a |
| 2x |
| a |
| 2x |
| 3 | x2•
| ||||
| 3 |
| ||
| a |
| 2x |
| 3 |
| ||
又因为函数f(x)的最小值为3,所以3
| 3 |
| ||
解得:a=2.
(Ⅱ)解法一:由(Ⅰ)得:|x-2|+|x+1|≤4.
原不等式等价于
|
|
|
解得-
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
解法二:由(Ⅰ)得:|x-2|+|x+1|≤4.
由绝对值的几何意义,可知该不等式即求数轴上到点2和点-1的距离之和不大于4的点的集合.
故原不等式解集为{x|-
| 3 |
| 2 |
| 5 |
| 2 |
点评:本小题主要考查平均值不等式、解含有绝对值号的不等式等基础知识,考查推理论证能力,考查化归与转化思想.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
执行如图所示的程序框图,输出S的值为( )


| A、-1 | B、1 | C、0 | D、-2014 |
已知i为虚数单位,复数z满足i3•z=1-3i,则z的共轭复数是( )
| A、-3+i | B、-3-i |
| C、3-i | D、3+i |
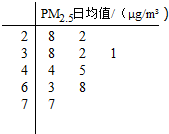 我国政府对PM2.5采用如下标准:
我国政府对PM2.5采用如下标准: