题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x+a,x<0}\\{-{x}^{2}+1+a,x≥0}\end{array}\right.$,且函数y=f(x)-x恰有3个不同的零点,则实数a的取值范围是( )| A. | (0,+∞) | B. | [-1,0) | C. | [-1,+∞) | D. | [-2,+∞) |
分析 利用二次函数的性质判断y=f(x)-x的单调性,根据零点个数判断y=f(x)-x在各单调区间端点的函数值的符号,列出不等式解出a的范围.
解答 解:令g(x)=f(x)-x=$\left\{\begin{array}{l}{-{x}^{2}-3x+a,x<0}\\{-{x}^{2}-x+1+a,x≥0}\end{array}\right.$,
则g(x)在(-∞,-$\frac{3}{2}$)上单调递增,在(-$\frac{3}{2}$,0)上单调递减,在(0,+∞)上单调递减,
∵g(x)有三个不同的零点,
∴$\left\{\begin{array}{l}{-\frac{9}{4}+\frac{9}{2}+a>0}\\{a<0}\\{1+a≥0}\end{array}\right.$,解得-1≤a<0.
故选B.
点评 本题考查了二次函数的性质,零点的存在性定理,属于中档题.

练习册系列答案
相关题目
15.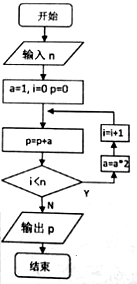 要使如图所示的程序框图输出的P不小于60,则输入的n值至少为( )
要使如图所示的程序框图输出的P不小于60,则输入的n值至少为( )
 要使如图所示的程序框图输出的P不小于60,则输入的n值至少为( )
要使如图所示的程序框图输出的P不小于60,则输入的n值至少为( )| A. | 5 | B. | 6 | C. | 7 | D. | 4 |
16.下列与y=|x|是同一函数的是( )
| A. | y=($\sqrt{x}$)2 | B. | y=$\sqrt{{x}^{2}}$ | C. | y=$\left\{\begin{array}{l}{x,(x>0)}\\{-x,(x<0)}\end{array}\right.$ | D. | y=x |
10.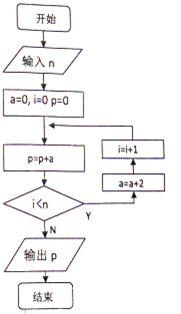 执行如图所示的程序框图,如果输入的n是6,那么输出的p是( )
执行如图所示的程序框图,如果输入的n是6,那么输出的p是( )
 执行如图所示的程序框图,如果输入的n是6,那么输出的p是( )
执行如图所示的程序框图,如果输入的n是6,那么输出的p是( )| A. | 12 | B. | 42 | C. | 30 | D. | 40 |
17.若函数f(x)=(x-2)(x+a)是偶函数,则实数a的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | ±2 |