题目内容
16.下列与y=|x|是同一函数的是( )| A. | y=($\sqrt{x}$)2 | B. | y=$\sqrt{{x}^{2}}$ | C. | y=$\left\{\begin{array}{l}{x,(x>0)}\\{-x,(x<0)}\end{array}\right.$ | D. | y=x |
分析 根据两个函数的定义域相同、对应关系也相同,即可判断它们是同一函数.
解答 解:对于A,函数y=${(\sqrt{x})}^{2}$=x(x≥0),与y=|x|(x∈R)的定义域不同,不是同一函数;
对于B,函数y=$\sqrt{{x}^{2}}$=|x|(x∈R),与y=|x|(x∈R)的定义域相同,对应关系也相同,是同一函数;
对于C,函数y=$\left\{\begin{array}{l}{x,x>0}\\{-x,x<0}\end{array}\right.$的定义域是{x|x≠0},与y=|x|的定义域不相同,不是同一个函数;
对于D,函数y=x,与函数y=|x|的对应关系不同,不是同一函数.
故选:B.
点评 本题考查了函数相等的定义与应用问题,即用“函数的定义域和解析式相同”,需要求出各个函数的定义域和对解析式进行化简后,进行判断.

练习册系列答案
相关题目
8.经过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为4$\sqrt{5}$,则直线l的方程为 ( )
| A. | x-2y+9=0或x+2y+3=0 | B. | 2x-y+9=0或2x+y+3=0 | ||
| C. | x+2y+3=0或x-2y+9=0 | D. | x+2y+9=0或2x-y+3=0 |
5.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x+a,x<0}\\{-{x}^{2}+1+a,x≥0}\end{array}\right.$,且函数y=f(x)-x恰有3个不同的零点,则实数a的取值范围是( )
| A. | (0,+∞) | B. | [-1,0) | C. | [-1,+∞) | D. | [-2,+∞) |
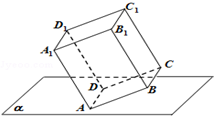 长方体ABCD-A1B1C1D1中,已知AA1=3,AB=AD=2,棱AD在平面α内,则长方体在平面α内的射影所构成的图形面积的取值范围是$4≤S≤2\sqrt{13}$.
长方体ABCD-A1B1C1D1中,已知AA1=3,AB=AD=2,棱AD在平面α内,则长方体在平面α内的射影所构成的图形面积的取值范围是$4≤S≤2\sqrt{13}$.