题目内容
17.已知A(1,-3),B(8,$\frac{1}{2}$)且A,B,C共线,则C点的坐标可能是( )| A. | (-9,1) | B. | (9,-1) | C. | (9,1) | D. | (-9,-1) |
分析 设出C点的坐标,求出向量$\overrightarrow{AB}$、$\overrightarrow{AC}$的坐标,根据共线向量的定义得到x-2y=7,代入方程验证即可.
解答 解:设C(x,y),
则$\overrightarrow{AC}$=(x-1,y+3),$\overrightarrow{AB}$=(7,$\frac{7}{2}$),
若A、B、C共线,
则$\overrightarrow{AC}$=λ$\overrightarrow{AB}$,
即$\left\{\begin{array}{l}{x-1=7λ}\\{y+3=\frac{7}{2}λ}\end{array}\right.$,
故x-2y=7①,
分别将A、B、C、D各个选项代入①得:C符合题意,
故选:C.
点评 本题考查了共线向量问题,设出C点坐标,得到二元一次方程是解题的关键,本题是一道基础题.

练习册系列答案
相关题目
5.sin14°cos74°-cos14°sin74°=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
12.若z+3-2i=4+i,则z等于( )
| A. | 1+i | B. | 1+3i | C. | -1-i | D. | -1-3i |
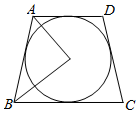 一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示)
一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示)