Question

如图，已知直线l₁：4x+y=0，直线l₂：x+y-1=0以及l₂上一点P（3，-2），求圆心在l₁上且与直线l₂相切于点P的圆的方程．

Answer 1

考点：圆的标准方程

专题：直线与圆

分析：法一：利用待定系数法即可求圆C的方程；
法二：根据直线和圆相切的等价条件，联立方程组求出圆心和半径即可．

解答： 解：法一：设圆的标准方程为（x-a）²+（y-b）²=r²，
∵圆C与直线l：x+y-1=0相切于点P（3，-2），且圆心在直线4x+y=0上，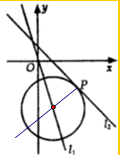
∴满足

b=-4a (3-a)2+(-2-b)2=r2 |a+b-1| 2 =r

，解得a=1，b=4，r=2

2

，
则圆的标准方程为（x-1）²+（y-4）²=8．
法二：过切点且与x+y-1=0垂直的直线方程为y+2=x-3，
即y=x-5与4x+y=0联立求得圆心为（1，-4），
则半径r=

(1-3)2+(-4+2)2

=2

2

，
则圆的标准方程为（x-1）²+（y-4）²=8．

点评：本题主要考查圆的标准方程的求解，以及直线和圆相切的应用，利用直线和圆的位置关系求出圆心和半径是解决本题的关键．