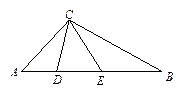题目内容
如图所示,在四面体ABCD中,E、F分别是线段AD、BC上的点, =
= =
= ,AB=CD=3,EF=
,AB=CD=3,EF= ,求AB、CD所成角的大小.
,求AB、CD所成角的大小.
 =
= =
= ,AB=CD=3,EF=
,AB=CD=3,EF= ,求AB、CD所成角的大小.
,求AB、CD所成角的大小.
AB与CD所成的角应是∠EGF的补角为60°
如图所示,在线段BD上取一点G,使 =
= .连接GF、GE、EF.
.连接GF、GE、EF.
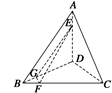
 =
=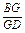 =
= =
= ,GE∥AB,且GE=
,GE∥AB,且GE=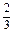 AB=2,
AB=2,
同理,GF∥CD,且GF=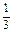 CD=1,
CD=1,
在△EGF中,cos∠EGF= =-
=- ,
,
∴∠EGF=120°.
由GF∥CD,GE∥AB可知,AB与CD所成的角应是∠EGF的补角为60°.
 =
= .连接GF、GE、EF.
.连接GF、GE、EF.
 =
=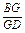 =
= =
= ,GE∥AB,且GE=
,GE∥AB,且GE=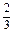 AB=2,
AB=2,同理,GF∥CD,且GF=
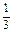 CD=1,
CD=1,在△EGF中,cos∠EGF=
 =-
=- ,
,∴∠EGF=120°.
由GF∥CD,GE∥AB可知,AB与CD所成的角应是∠EGF的补角为60°.

练习册系列答案
相关题目
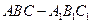 的各条棱长均为
的各条棱长均为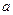 ,
,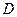 是侧棱
是侧棱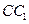 的中点.
的中点.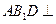 平面
平面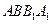 ;
;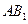 与
与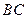 所成角的余弦值;
所成角的余弦值;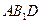 与平面
与平面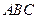 所成二面角(锐角)的大小.
所成二面角(锐角)的大小.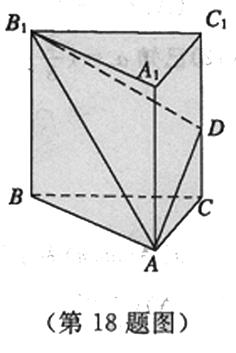
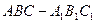 中,
中,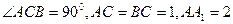 ,点N是
,点N是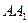 的中点,求二面角
的中点,求二面角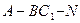 的平面角的大小。
的平面角的大小。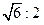 ,则其侧面与底面的夹角为( ).
,则其侧面与底面的夹角为( ). 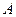 、
、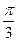 ;
; 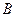 、
、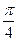 ;
; 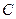 、
、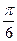 ;
; 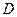 、
、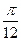 .
.