题目内容
(本小题满分12分)
如图所示,直三棱柱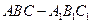 的各条棱长均为
的各条棱长均为 ,
, 是侧棱
是侧棱 的中点.
的中点.
(l)求证:平面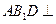 平面
平面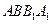 ;
;
(2)求异面直线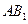 与
与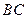 所成角的余弦值;
所成角的余弦值;
(3)求平面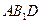 与平面
与平面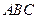 所成二面角(锐角)的大小.
所成二面角(锐角)的大小.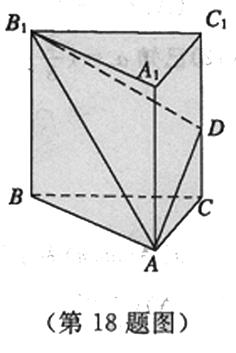
如图所示,直三棱柱
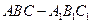 的各条棱长均为
的各条棱长均为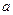 ,
,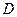 是侧棱
是侧棱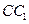 的中点.
的中点.(l)求证:平面
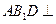 平面
平面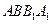 ;
;(2)求异面直线
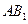 与
与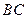 所成角的余弦值;
所成角的余弦值;(3)求平面
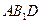 与平面
与平面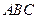 所成二面角(锐角)的大小.
所成二面角(锐角)的大小.
(1)见解析(2)异面直线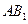 与
与 所成角的余弦值为
所成角的余弦值为 (3)所求二面角的大小为
(3)所求二面角的大小为
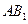 与
与 所成角的余弦值为
所成角的余弦值为 (3)所求二面角的大小为
(3)所求二面角的大小为
(l)证明:取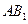 的中点
的中点 ,
, 的中点
的中点 .连结
.连结 .
.

故 .又
.又 四边形
四边形 为平行四边形,
为平行四边形,
 ∥
∥ .又三棱柱
.又三棱柱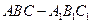 是直三棱柱.△
是直三棱柱.△ 为正三角形.
为正三角形. 平面
平面 ,
, ,而
,而 ,
, 平面
平面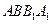 ,
, 又
又 ∥
∥ ,
,
 平面
平面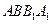 .
.
又
 平面
平面 .所以平面
.所以平面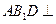 平面
平面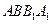 .…………………………4分
.…………………………4分
(2)建立如图所示的空间直角坐标系,则

设异面直线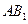 与
与 所成的角为
所成的角为 ,则
,则

故异面直线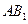 与
与 所成角的余弦值为
所成角的余弦值为
(3)由(2)得
设 为平面
为平面 的一个法向量.
的一个法向量.
由 得,
得,
即 ……………………………………6分
……………………………………6分
显然平面 的一个法向量为
的一个法向量为 .
.
则 ,故
,故 .
.
即所求二面角的大小为 ………………12分
………………12分
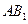 的中点
的中点 ,
, 的中点
的中点 .连结
.连结 .
.
故
 .又
.又 四边形
四边形 为平行四边形,
为平行四边形,
 ∥
∥ .又三棱柱
.又三棱柱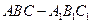 是直三棱柱.△
是直三棱柱.△ 为正三角形.
为正三角形. 平面
平面 ,
, ,而
,而 ,
, 平面
平面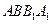 ,
, 又
又 ∥
∥ ,
,
 平面
平面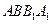 .
.又

 平面
平面 .所以平面
.所以平面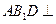 平面
平面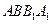 .…………………………4分
.…………………………4分(2)建立如图所示的空间直角坐标系,则

设异面直线
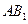 与
与 所成的角为
所成的角为 ,则
,则
故异面直线
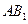 与
与 所成角的余弦值为
所成角的余弦值为
(3)由(2)得

设
 为平面
为平面 的一个法向量.
的一个法向量.由
 得,
得,
即
 ……………………………………6分
……………………………………6分显然平面
 的一个法向量为
的一个法向量为 .
.则
 ,故
,故 .
.即所求二面角的大小为
 ………………12分
………………12分
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
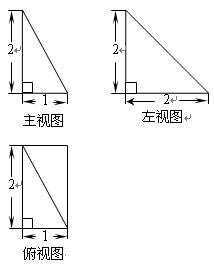
 的直观图和三视图如图所示,
的直观图和三视图如图所示, 是
是 的中点.
的中点. 是
是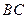 上任一点,求证:
上任一点,求证: ;
; ,
, 交于点
交于点 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,若
中,若 ,
, ,则异面直线
,则异面直线 与
与 所成的角等于
所成的角等于 如图,正方体
如图,正方体 中,
中, 、
、 、
、
 ,
, ,
, 的中点,
的中点, 为
为 上的任意一点,
上的任意一点, 平面
平面 ;
; 平面
平面 与
与 所成的角.
所成的角. ,
, ,沿对角线AC将矩形折成直二面
,沿对角线AC将矩形折成直二面 ,,则B与D之间的距离是 。
,,则B与D之间的距离是 。
 ,经过这三点的小圆的周长为
,经过这三点的小圆的周长为 ,则这个球的表面积为 ( )
,则这个球的表面积为 ( )



 =
= =
= ,AB=CD=3,EF=
,AB=CD=3,EF= ,求AB、CD所成角的大小.
,求AB、CD所成角的大小.
 内射影长的2倍,则AB与平面
内射影长的2倍,则AB与平面


