题目内容
函数y=f(x)的图象向右平移
个单位后与函数y=cos(2x-
)的图象重合,则y=f(x)的解析式为( )
| π |
| 6 |
| π |
| 2 |
A、y=cos(2x-
| ||
B、y=cos(2x+
| ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由条件利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答:
解:由题意可得,把函数y=cos(2x-
)=sin2x的图象向左平移
个单位后,
可得函数y=f(x)=sin2(x+
)=sin(2x+
)的图象,
故选:C.
| π |
| 2 |
| π |
| 6 |
可得函数y=f(x)=sin2(x+
| π |
| 6 |
| π |
| 3 |
故选:C.
点评:本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,体现了转化的数学思想,属于基础题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
设△ABC的内角A,B,C的对边分别为a,b,c,且(a+b+c)(a-b-c)=-3bc.则A=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
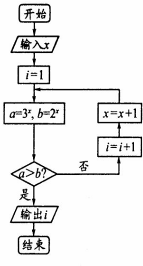
执行如图所示的程序框图,若输入的x的值为-
,则输出的i的值为( )
| 3 |
| 2 |

| A、4 | B、3 | C、2 | D、1 |
 如图是某正五棱台灯罩的俯视图,在A,B,C,D,E五个侧面上装裱3种不同的透明中国山水画,相邻区域的中国山水画不同,则不同的装裱方案数是
如图是某正五棱台灯罩的俯视图,在A,B,C,D,E五个侧面上装裱3种不同的透明中国山水画,相邻区域的中国山水画不同,则不同的装裱方案数是