题目内容
18.若实数x,y满足x2+2y2+xy=1,求x+2y的最大值.分析 设x+2y=m,从而化简x2+2y2+xy=1为4y2-3my+m2-1=0,从而利用判别式求解.
解答 解:设x+2y=m,则x=m-2y,
∵x2+2y2+xy=1,
∴(m-2y)2+2y2+(m-2y)y=1,
即4y2-3my+m2-1=0,
故△=9m2-4×4×(m2-1)≥0,
故m2≤$\frac{16}{7}$,
故m的最大值,即x+2y的最大值为$\frac{4\sqrt{7}}{7}$.
点评 本题考查了函数的性质与应用,同时考查了函数与方程的关系应用及判别式法的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.设集合M={-1,1,2,3,4,5},B={x|x<3},则M∩N=( )
| A. | {3,4,5} | B. | {4,5} | C. | {-1,1} | D. | {-1,1,2} |
6.△DEF的外接圆的圆心为O,半径R=4,如果$\overrightarrow{OD}$+$\overrightarrow{DE}$+$\overrightarrow{DF}$=$\overrightarrow{0}$,且|$\overrightarrow{OD}$|=|$\overrightarrow{DF}$|,则向量$\overrightarrow{EF}$在$\overrightarrow{FD}$方向上的投影为( )
| A. | 6 | B. | -6 | C. | $2\sqrt{3}$ | D. | $-2\sqrt{3}$ |
3.已知集合A={x|x+1>0},B={x|x2-2≤0},则A∩B=( )
| A. | {x|x$≥-\sqrt{2}$} | B. | {x|-$\sqrt{2}$≤x≤-1} | C. | {x|-$\sqrt{2}≤x≤\sqrt{2}$} | D. | {x|-1$≤x≤\sqrt{2}$} |
8.已知定义域为R的函数f(x)在(2,+∞)上单调递减,且y=f(x+2)为偶函数,则关于x的不等式f(2x-1)-f(x+1)>0的解集为( )
| A. | (-∞,-$\frac{4}{3}$)∪(2,+∞) | B. | (-$\frac{4}{3}$,2) | C. | (-∞,$\frac{4}{3}$)∪(2,+∞) | D. | ($\frac{4}{3}$,2) |
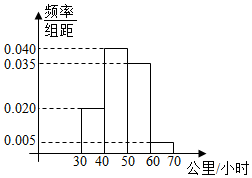 某公路的一个下穿隧道限速60公里/小时,现监控了200辆经过该隧道的车速,将这200个数据作成了频率分布直方图(如图).
某公路的一个下穿隧道限速60公里/小时,现监控了200辆经过该隧道的车速,将这200个数据作成了频率分布直方图(如图).