题目内容
已知函数f(x)=
(1)当0≤a≤4时,试判断函数f(x)的单调性;
(2)当a=0时,对于任意的x∈(1,t],恒有tf(x)-xf(t)≥f(x)-f(t),求t的最大值.
| ex |
| x2-ax+a |
(1)当0≤a≤4时,试判断函数f(x)的单调性;
(2)当a=0时,对于任意的x∈(1,t],恒有tf(x)-xf(t)≥f(x)-f(t),求t的最大值.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:函数的性质及应用,导数的综合应用
分析:(1)求出导数,f′(x)=
=
分类讨论判断单调性,
(2)把不等式tf(x)-xf(t)≥f(x)-f(t),转化为
≥
,
构造函数g(x)=
=
,即证明g(t)为g(x)的最小值,即可求出t的范围.
| ex[x2-(a+2)x+2a] |
| (x2-ax+a)2 |
| ex(x-a)(x-2) |
| (x2-ax+a)2 |
(2)把不等式tf(x)-xf(t)≥f(x)-f(t),转化为
| f(x) |
| x-1 |
| f(t) |
| t-1 |
构造函数g(x)=
| f(x) |
| x-1 |
| ex |
| x2(x-1) |
解答:
解:(1)f′(x)=
=
当a=0时,f(x)=
,f′(x)=
,
故f(x)在区间(-∞,0),(2,+∞)上单调递增,在(0,2)上单调递减;
当a=4时,f(x)=
,f′(x)=
,
故f(x)在区间(-∞,2),(4,+∞)上单调递增,在(2,4)上单调递减;
当0<a<4时,恒有x2-ax+a<0,
当0<a<2时,f(x)在(-∞,a),(2,+∞)上单调递增,在(a,2)上单调递减;
当a=2时,f(x)在区间(-∞,+∞)上单调递增
当2<a<4时,f(x)在(-∞,2),(a,+∞)上单调递增,在(2,a)上单调递减;
(2)tf(x)-xf(t)≥f(x)-f(t)
(t-1)f(x)≥(x-1)f(t)
≥
解法一:设函数g(x)=
=
,
即g(x)≥g(t)在(1,t]上恒成立.
即g(t)为g(x)的最小值.
g′(x)=
.
故g(x)在区间(1,2+
)上单调递减,在区间(2+
,+∞)单调递增.
故t≤2+
,tmax=2+
解法二:
≥
即(x,f(x))与点(1,0)连线斜率的最小值在x=t时取到.
设tmax=t
则
=f′(t),
即
=
t2-4t+2=0,即t=2±
,
又t>1,
故t=2+
| ex[x2-(a+2)x+2a] |
| (x2-ax+a)2 |
| ex(x-a)(x-2) |
| (x2-ax+a)2 |
当a=0时,f(x)=
| ex |
| x2 |
| ex(x-2) |
| x3 |
故f(x)在区间(-∞,0),(2,+∞)上单调递增,在(0,2)上单调递减;
当a=4时,f(x)=
| ex |
| (x-2)2 |
| ex(x-4) |
| (x-2)3 |
故f(x)在区间(-∞,2),(4,+∞)上单调递增,在(2,4)上单调递减;
当0<a<4时,恒有x2-ax+a<0,
当0<a<2时,f(x)在(-∞,a),(2,+∞)上单调递增,在(a,2)上单调递减;
当a=2时,f(x)在区间(-∞,+∞)上单调递增
当2<a<4时,f(x)在(-∞,2),(a,+∞)上单调递增,在(2,a)上单调递减;
(2)tf(x)-xf(t)≥f(x)-f(t)
(t-1)f(x)≥(x-1)f(t)
| f(x) |
| x-1 |
| f(t) |
| t-1 |
解法一:设函数g(x)=
| f(x) |
| x-1 |
| ex |
| x2(x-1) |
即g(x)≥g(t)在(1,t]上恒成立.
即g(t)为g(x)的最小值.
g′(x)=
| ex(x2-4x+2) |
| x3(x-1)2 |
故g(x)在区间(1,2+
| 2 |
| 2 |
故t≤2+
| 2 |
| 2 |
解法二:
| f(x) |
| x-1 |
| f(t) |
| t-1 |
即(x,f(x))与点(1,0)连线斜率的最小值在x=t时取到.
设tmax=t
则
| f(t) |
| t-1 |
即
| et |
| t2(t-1) |
| et(t-2) |
| t3 |
t2-4t+2=0,即t=2±
| 2 |
又t>1,
故t=2+
| 2 |
点评:本题综合考察了导数在证明单调性,证明不等式,求解函数最值中的应用,属于难题.

练习册系列答案
相关题目
不等式|x-m|<1的充分不必要条件是“
<x<
”,则实数m的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
A、[-
| ||||
B、(-∞,-
| ||||
C、(-
| ||||
D、(-
|
已知集合A={x|1≤x≤2},集合B={x|x2-x>0},则( )
| A、A∪B=R |
| B、A=B |
| C、B⊆A |
| D、A∩B=(1,2] |
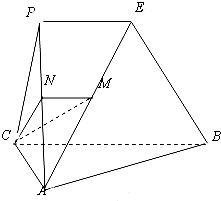 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥BC,过BC作平面交AP、AE分别于点M、N.
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥BC,过BC作平面交AP、AE分别于点M、N.