题目内容
3.在△ABC中,a、b、c分别是角A、B、C的对边,△ABC的面积为S,(a2+b2)tanC=8S,则$\frac{si{n}^{2}A+si{n}^{2}B}{si{n}^{2}C}$=2.分析 由已知,利用三角形面积公式,余弦定理可得a2+b2=2c2,利用正弦定理化简所求即可计算得解.
解答 解:由于:(a2+b2)tanC=8S,
可得:a2+b2=4abcosC=4ab•$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,
可得:a2+b2=2c2,
则:$\frac{si{n}^{2}A+si{n}^{2}B}{si{n}^{2}C}$=$\frac{{a}^{2}+{b}^{2}}{{c}^{2}}$=2.
故答案为:2.
点评 本题主要考查了三角形面积公式,余弦定理,正弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
11.下列函数中,既是偶函数又是(0,+∞)上的增函数的是( )
| A. | y=x3 | B. | y=2|x| | C. | y=-x2 | D. | y=log3(-x) |
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线l:x-y+2=0平行,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{10}$ |
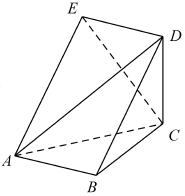 如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.
如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.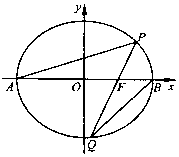 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左、右顶点分别为A,B,过右焦点F的直线l与椭圆C交于P,Q两点(点P在x轴上方).
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左、右顶点分别为A,B,过右焦点F的直线l与椭圆C交于P,Q两点(点P在x轴上方).