题目内容
14.已知定义在R上的函数f(x)满足f(x)=$\left\{\begin{array}{l}{x^2}+2,x∈[0,1)\\ 2-{x^2},x∈[-1,0)\end{array}$,且f(x+2)=f(x),g(x)=$\frac{2x+5}{x+2}$,则方程f(x)=g(x)在区间[-6,2]上的所有实根之和为( )| A. | -5 | B. | -7 | C. | -9 | D. | -11 |
分析 将方程根的问题转化为函数图象的交点问题,由图象读出即可.
解答 解:∵f(x)=$\left\{\begin{array}{l}{x^2}+2,x∈[0,1)\\ 2-{x^2},x∈[-1,0)\end{array}$,且f(x+2)=f(x),
∴f(x-2)-2=$\left\{\begin{array}{l}{{x}^{2},x-2∈[0,1)}\\{{-x}^{2},x-2∈[-1,0)}\end{array}\right.$,
又g(x)=$\frac{2x+5}{x+2}$,则g(x)=2+$\frac{1}{x+2}$,
∴g(x-2)-2=$\frac{1}{x}$,
当x≠2k-1,k∈Z时,
上述两个函数都是关于(-2,2)对称, ;
;
由图象可得:方程f(x)=g(x)在区间[-6,2]上的实根有3个,
x1满足-5<x1<-4,x2=-3,x4满足0<x3<1,x1+x3=-4,
∴方程f(x)=g(x)在区间[-6,2]上的所有实根之和为-7.
故选:B.
点评 本题考查函数的零点与方程根的关系以及数形结合的思想,数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质.

练习册系列答案
相关题目
4.下列函数中,值域为[0,+∞)的偶函数是( )
| A. | y=x2-1 | B. | y=|x| | C. | y=lgx | D. | y=cosx |
9.在平面直角坐标系xOy中,圆C的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=-1+sinθ\end{array}\right.(θ$为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的圆心的极坐标为( )
| A. | $(1,-\frac{π}{2})$ | B. | (1,π) | C. | (0,-1) | D. | $(1,\frac{π}{2})$ |
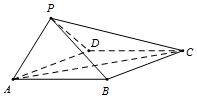 如图,菱形ABCD与等边△PAD所在的平面相互垂直,AD=2,∠DAB=60°.
如图,菱形ABCD与等边△PAD所在的平面相互垂直,AD=2,∠DAB=60°. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P是线段BD1上的动点.当△PAC在平面DC1,BC1,AC上的正投影都为三角形时,将它们的面积分别记为S1,S2,S3.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P是线段BD1上的动点.当△PAC在平面DC1,BC1,AC上的正投影都为三角形时,将它们的面积分别记为S1,S2,S3.