题目内容
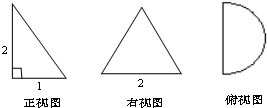
某几何体的三视图如图所示,则该几何体的体积为( )

A、
| ||
B、
| ||
| C、π | ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:利用三视图判断几何体的形状为一个底面半径为1,高为2的半圆锥,然后通过三视图的数据求解几何体的体积.
解答:
解:几何体为圆锥被轴截面分割出的半个圆锥体,底面是半径为1的半圆,高为2.
所以体积V=
•
•π•12•2=
.
故选:B.
所以体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
故选:B.
点评:本题考查几何体与三视图的对应关系,几何体体积的求法,考查空间想象能力与计算能力.

练习册系列答案
相关题目
要得到y=sin(
x+
)的图象,需要将y=sin
x( )
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
如果AB<0,且BC<0,那么直线Ax+By+C=0不通过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知角α的终边在函数y=x的图象上,则1-2sinαcosα-3cos2α的值为( )
A、±
| ||
B、±
| ||
C、
| ||
D、-
|
已知双曲线的方程为
-
=-1,F1,F2是其两个焦点,点P为双曲线上一点,|PF1|=5,则|PF2|等于( )
| x2 |
| 12 |
| y2 |
| 4 |
| A、1或9 | ||||
| B、9 | ||||
C、5+4
| ||||
D、5+4
|
已知三角形ABC的三点顶点的A、B、C及平面内一点P满足
+
+
=
,则△ABP与△ABC的面积比为( )
| PA |
| PB |
| PC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|x2+x-2=0},B={x|ax=1},若A∩B=B,则a=( )
A、-
| ||
| B、2或-1 | ||
| C、-2或1或0 | ||
D、-
|
等比数列{an}中,若a2+a4=20,a3+a5=40,则a6=( )
| A、32 | B、64 | C、128 | D、81 |