题目内容
正四棱锥的底面边长为2cm,高为3cm,则该四棱锥的表面积为 cm2.
考点:棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:由已知中正四棱锥的底面边长为2cm,高为3cm,求出棱锥的侧高,进而求出棱锥的侧面积,加上底面积后,可得答案.
解答:
解:如下图所示:正四棱锥S-ABCD中,AB=BC=CD=AD=2cm,S0=3cm,E为BC中点,
在Rt△SOE中,OE=
AB=1cm,
则侧高SE=
=
cm,

故棱锥的表面积S=2×2+4×(
×2×
)=4+4
cm2.
故答案为:4+4
在Rt△SOE中,OE=
| 1 |
| 2 |
则侧高SE=
| SO2+OE2 |
| 10 |

故棱锥的表面积S=2×2+4×(
| 1 |
| 2 |
| 10 |
| 10 |
故答案为:4+4
| 10 |
点评:本题考查的知识点是棱锥的表面积,其中求出棱锥的侧高是解答的关键.

练习册系列答案
相关题目
已知数列{an}的前n项和为Sn=1-5+9-13+17-21+…+(-1)n+1(4n-3),则S15+S22的值是( )
| A、-73 | B、73 |
| C、-15 | D、15 |
某几何体的三视图如图所示,则该几何体的体积为( )
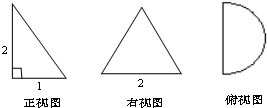

A、
| ||
B、
| ||
| C、π | ||
D、
|