题目内容
已知双曲线的方程为
-
=-1,F1,F2是其两个焦点,点P为双曲线上一点,|PF1|=5,则|PF2|等于( )
| x2 |
| 12 |
| y2 |
| 4 |
| A、1或9 | ||||
| B、9 | ||||
C、5+4
| ||||
D、5+4
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出双曲线的标准方程,结合双曲线的定义建立方程即可得到结论.
解答:
解:∵双曲线的方程为
-
=-1,即
-
=1,
∴a2=4,b2=12,c2=16,
则a=2,c=4,
∵|PF1|=5<a+c,
∴点P在双曲线的左支上,
则由双曲线的定义可知|PF2|-|PF1|=2a=4,
即|PF2|=4+|PF1|=4+5=9,
故选:B
| x2 |
| 12 |
| y2 |
| 4 |
| y2 |
| 4 |
| x2 |
| 12 |
∴a2=4,b2=12,c2=16,
则a=2,c=4,
∵|PF1|=5<a+c,
∴点P在双曲线的左支上,
则由双曲线的定义可知|PF2|-|PF1|=2a=4,
即|PF2|=4+|PF1|=4+5=9,
故选:B
点评:本题主要考查双曲线的定义和方程,注意根据条件确定P的位置是解决本题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
| AB |
| CB |
A、
| ||
B、
| ||
C、
| ||
D、2
|
下列命题中不正确的是( )
| A、若ξ~B(n,p),则Eξ=np,Dξ=np(1-p) |
| B、E(aξ+b)=aEξ+b |
| C、D(aξ+b)=aDξ |
| D、Dξ=Eξ 2-(Eξ)2 |
某几何体的三视图如图所示,则该几何体的体积为( )
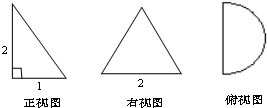

A、
| ||
B、
| ||
| C、π | ||
D、
|
设a,b∈R,且a+b=2,则(
)a+(
)b的最小值是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
将函数y=sin(x-
)图象向左平移
个单位,所得函数图象的一条对称轴的方程是( )
| π |
| 6 |
| π |
| 4 |
A、x=
| ||
B、x=
| ||
C、2
| ||
D、x=-
|
若向量
=(x-2,3)与向量
=(1,y+2)相等,则( )
| a |
| b |
| A、x=1,y=3 |
| B、x=3,y=1 |
| C、x=1,y=-5 |
| D、x=5,y=-1 |
函数f(x)=
(0≤x≤2π)的值域为( )
| sinx-1 | ||
|
| A、[-1,0] | ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
