题目内容
已知三角形ABC的三点顶点的A、B、C及平面内一点P满足
+
+
=
，则△ABP与△ABC的面积比为（ ）
| PA |
| PB |
| PC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：向量在几何中的应用
专题：平面向量及应用
分析：先将条件
+
+
=
变形为
+
+
=
-
，即
=-2
，从而确定P点是边AC上更靠近A点的三等分点，则问题迎刃而解．
| PA |
| PB |
| PC |
| AB |
| PA |
| PB |
| PC |
| PB |
| PA |
| PC |
| PA |
解答：
解：∵
+
+
=
，
∴
+
+
=
-
，即
=-2
，
∴P是AC的三等分点，且|PC|=2|PA|，
∴|PA|=
|AC|，
又∵△ABP的AP边与△ABC的AC边上的高相等，
∴S△ABP：S△ABC=|AP|：|AC|=
，
故选C
| PA |
| PB |
| PC |
| AB |
∴
| PA |
| PB |
| PC |
| PB |
| PA |
| PC |
| PA |
∴P是AC的三等分点，且|PC|=2|PA|，
∴|PA|=
| 1 |
| 3 |
又∵△ABP的AP边与△ABC的AC边上的高相等，
∴S△ABP：S△ABC=|AP|：|AC|=
| 1 |
| 3 |
故选C
点评：熟练的将
+
+
=
，中的向量化成同一起点P的向量是解决本题的关键，然后一旦找到了A，P，C三点的关系，问题就容易多了．
| PA |
| PB |
| PC |
| AB |
练习册系列答案
相关题目
有五条线段长度分别为1，3，5，7，9，从这5条线段中任取3条，则所取3条线段能构成一个锐角三角形的概率为（ ）
A、
| ||
B、
| ||
| C、0 | ||
D、
|
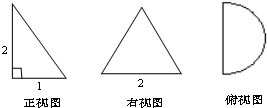
某几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
| C、π | ||
D、
|
椭圆C：
+
=1（a＞b＞0）和双曲线D：
-
=1（A＞0，B＞0）有相同的焦点F1、F2，椭圆C和双曲线D在第一象限内的交点为P，且PF2垂直于x轴．设椭圆的离心率为e1，双曲线D的离心率为e2，则e1e2等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| A2 |
| y2 |
| B2 |
| A、1 | ||
B、
| ||
C、
| ||
| D、不确定 |
将函数y=sin（x-
）图象向左平移
个单位，所得函数图象的一条对称轴的方程是（ ）
| π |
| 6 |
| π |
| 4 |
A、x=
| ||
B、x=
| ||
C、2
| ||
D、x=-
|
要得到函数y=cosx的图象，只需将函数y=cos（x+
）的图象沿x轴（ ）
| π |
| 4 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
方程y=k（x-2）表示（ ）
| A、过点（-2，0）的一切直线 |
| B、过点（2，0）的一切直线 |
| C、过点（2，0）且不垂直于x轴的一切直线 |
| D、过点（2，0）且除去x轴的一切直线 |
在回归模型中，预报变量的值与下列哪些因素有关（ ）
| A、受解释变量的影响与随机误差无关 |
| B、受随机误差的影响与解释变量无关 |
| C、与总偏差平方和有关与残差无关 |
| D、与解释变量和随机误差的总效应有关 |