题目内容
已知角α的终边在函数y=x的图象上,则1-2sinαcosα-3cos2α的值为( )
A、±
| ||
B、±
| ||
C、
| ||
D、-
|
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:角α的终边在函数y=x的图象上,知tanα=1,原式转化为1-2sinαcosα-3cos2α=
,弦化切即可求得答案.
| sin2α-2sinαcosα-2cos2α |
| sin2α+cos2α |
解答:
解:依题意知,tanα=1,
1-2sinαcosα-3cos2α
=
=
=
=-
,
故选:D.
1-2sinαcosα-3cos2α
=
| sin2α-2sinαcosα-2cos2α |
| sin2α+cos2α |
| tan2α-2tanα-2 |
| tan2α+1 |
| 1-2-2 |
| 1+1 |
| 3 |
| 2 |
故选:D.
点评:本题考查任意角的三角函数的定义,着重考查同角三角函数间的关系的应用,弦化切是关键,考查运算能力,属于中档题.

练习册系列答案
相关题目
为了了解儿子与其父亲身高的关系,随机抽取5对父子的身高数据如下:
则y关于x的线性回归方程必通过以下哪个点( )
| 父亲身高x | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y | 175 | 175 | 176 | 177 | 177 |
| A、(174,175) |
| B、(176,175) |
| C、(174,176) |
| D、(176,176) |
有五条线段长度分别为1,3,5,7,9,从这5条线段中任取3条,则所取3条线段能构成一个锐角三角形的概率为( )
A、
| ||
B、
| ||
| C、0 | ||
D、
|
已知锐角α,β,满足cosα=
,cos(α+β)=-
,则cosβ=( )
| 3 |
| 5 |
| 5 |
| 13 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
某几何体的三视图如图所示,则该几何体的体积为( )
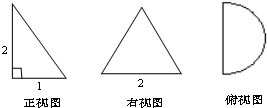

A、
| ||
B、
| ||
| C、π | ||
D、
|
椭圆C:
+
=1(a>b>0)和双曲线D:
-
=1(A>0,B>0)有相同的焦点F1、F2,椭圆C和双曲线D在第一象限内的交点为P,且PF2垂直于x轴.设椭圆的离心率为e1,双曲线D的离心率为e2,则e1e2等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| A2 |
| y2 |
| B2 |
| A、1 | ||
B、
| ||
C、
| ||
| D、不确定 |
要得到函数y=cosx的图象,只需将函数y=cos(x+
)的图象沿x轴( )
| π |
| 4 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
在△ABC中,A=60°,b=1,且面积为
,则
=( )
| 3 |
| 2a+2b-2c |
| sinA+sinB-sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、4
|