题目内容
12.(-$\frac{1}{4}$)-2+${8}^{\frac{2}{3}}$+$(\frac{1}{32})^{-\frac{2}{5}}$+$\root{4}{(-4)^{2}}$=( )| A. | 26 | B. | -6 | C. | 24 | D. | 20 |
分析 利用有理指数幂的运算性质计算(-$\frac{1}{4}$)-2+${8}^{\frac{2}{3}}$+$(\frac{1}{32})^{-\frac{2}{5}}$+$\root{4}{(-4)^{2}}$=16+${2}^{3×\frac{2}{3}}$+$(\frac{1}{2})^{5×(-\frac{2}{5})}$+$\root{4}{{2}^{4}}$=16+4+4+2=26.
解答 解:(-$\frac{1}{4}$)-2+${8}^{\frac{2}{3}}$+$(\frac{1}{32})^{-\frac{2}{5}}$+$\root{4}{(-4)^{2}}$
=16+${2}^{3×\frac{2}{3}}$+$(\frac{1}{2})^{5×(-\frac{2}{5})}$+$\root{4}{{2}^{4}}$
=16+4+4+2
=26,
故选:A.
点评 本题考查了有理指数幂的运算性质的应用.

练习册系列答案
相关题目
2.已知tanα,tanβ为方程x2-5x+2=0的解,则tan(α+β)的值为( )
| A. | $\frac{1}{5}$ | B. | 5 | C. | -5 | D. | -1 |
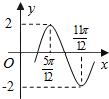 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).