题目内容
1.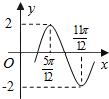 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).
分析 由图象可得A=2,结合周期公式可得ω=2,代入点($\frac{5π}{12}$,2)结合可得φ的范围可得φ的值,可得解析式.
解答 解:由图象可得A=2,$\frac{2π}{ω}$=2($\frac{11π}{12}$-$\frac{5π}{12}$),
解得ω=2,∴y=2sin(2x+φ),
代入点($\frac{5π}{12}$,2)可得2=2sin(2×$\frac{5π}{12}$+φ),
结合|φ|≤$\frac{π}{2}$可得φ=-$\frac{π}{3}$,
∴y=2sin(2x-$\frac{π}{3}$),
故答案为:y=2sin(2x-$\frac{π}{3}$)
点评 本题考查三角函数的图象和系数的意义,属基础题.

练习册系列答案
相关题目
12.(-$\frac{1}{4}$)-2+${8}^{\frac{2}{3}}$+$(\frac{1}{32})^{-\frac{2}{5}}$+$\root{4}{(-4)^{2}}$=( )
| A. | 26 | B. | -6 | C. | 24 | D. | 20 |
6.使f(x)=sin(2x+θ)-$\sqrt{3}$cos(2x+θ)为偶函数,且在[$\frac{π}{4}$,$\frac{π}{3}$]上是减函数的θ的一个值是( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{6}$ |
10.已知不等式组$\left\{\begin{array}{l}{{x}^{2}-x-2>0}\\{2{x}^{2}+(5+2k)x+5k<0}\end{array}\right.$的整数解只有-2,则k的范围是( )
| A. | -3≤k<2 | B. | -2≤k≤-1 | C. | -3<k<-1 | D. | -3≤k<0 |